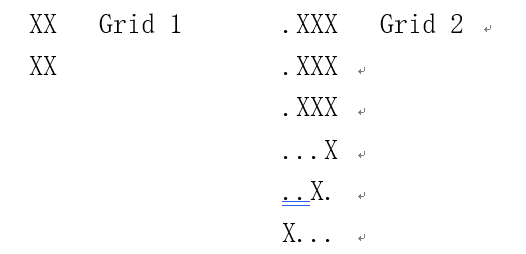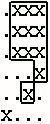# NENUOJ 之 算法2搜索E
# 前言
这一章是搜索相关,搜索需要有很强的“转移”的意识,你要能把题目变成一颗“树”,然后在这棵”树“上完成你的搜索。
搜索和动态规划是相似的,想办法分类讨论+分解吧~
# E001 数的划分 (opens new window)
# 题目描述
将整数n分成k份,且每份不能为空,任意两种分法不能相同(不考虑顺序)。 例如:n=7,k=3,下面三种分法被认为是相同的。 1,1,5;1,5,1;5,1,1; 问有多少种不同的分法。
# 输入
每组数据由一行上的2个整数n,k构成(6<n≤200,2≤k≤6)。
# 输出
对每组测试数据,输出不同的分法整数。
# 样例输入 复制
7 3# 样例输出 复制
4
# 思路:
这道题我们要怎么搜索呢?
搜索其实我们通常最基本最入门的做法,就是枚举所有的情况。
枚举就是搜索的入门!我们可以想办法枚举所有情况!
比如枚举7分成3份,我们枚举1 1 5、1 2 4、1 3 3、2 2 3这四种情况。同时我们保证这几个数字是一个比一个大(大于等于)就不会出现重复的情况。
也就是什么,我们每个数字都可以在1 ~ 7之间枚举【也就是1~n】,同时这3个数字【也就是这k个数字】要满足后一个大于等于前一个【保证不重复】。
所以我们可以写一个DFS,记录我们枚举到了第几个数字,和前一个数字的值【start用来让下一个数字不会小于前一个数字】以及所有数字之和,让我们最后的和可以是n,并且确实递归了k次【也就是划分了k次】
动态规划的思路:
其实我们可以分类讨论出两种情况,一个就是 这k个盘子里至少有一个盘子是1 和 这k个盘子里没有1(都是大于1的)
我们用 $f[i][j]$ 表示将 $ i $ 拆分成 $ j $ 份的方案数,那么我们就可以把这个拆成两部分,即 $f[i - 1][j - 1]$ 【这是至少有1个盘子是1,所以其他 $j - 1$ 个盘子里放的就是 $i-1$ 个,还有 $f[i - j][j]$ 【这是先给每个盘子都先放了1个,也就是少了 $j$ 个,剩下 $i-j$ 个,划分给 $j$ 个盘子。
所以总而言之,$f[i][j] = f[i-1][j-1] + f[i-j][j]$。
但是如果 i < j 的时候,我们不存在这种情况【题目保证了数字要比划分数多】,所以赋值为0就好。【或者不管】
# 代码C++ DFS版本:
#include<bits/stdc++.h>
using namespace std;
int n,k;
int cnt = 0;
// dfs用来递归枚举每一种分法
void dfs(int level,int start,int sum) {
// 如果已经分成了k份
if (level == k) {
// 确保所有分的总和等于n
if (sum == n) {
cnt++;
}
return;
}
// 从start开始,枚举每个可能的分数【start保证了后一个数大于等于前一个数】
for (int i = start;i <= n - sum;i++) {
dfs(level + 1,i,sum + i);
}
}
int main() {
cin >> n >> k;
dfs(0,1,0); // 从第0层开始,起始数字为1,初始和为0
cout << cnt << "\n";
return 0;
}
# 代码C++ dp版本:
#include<bits/stdc++.h>
using namespace std;
int f[201][201]; // f[i][j] 表示将 i 拆分成 j 份的方案数
int main() {
int n,k;
cin >> n >> k;
for (int i = 1;i <= n;i++) {
// 将 i 拆成 1 份,只有一种方法,就是 i 本身
f[i][1] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 2; j <= k; j++) {
if (i >= j) {
// 如果 i >= j,才有可能将 i 拆成 j 份
f[i][j] = f[i-1][j-1] + f[i-j][j];
} else {
// 如果 i < j,只能拆成 j-1 份
// 这里写不写都行
f[i][j] = 0;
}
}
}
// 将 n 拆成 k 份的不同分法数
cout << f[n][k] << "\n";
return 0;
}
# E002 闪避湖泊 (opens new window)
# 题目描述
农夫约翰的农场在最近的一场暴风雨中被水淹没。但保险公司仅根据他得农场中最大的“湖泊”的大小赔偿一个数额。 农场可表示为N行M列的长方形网格,(1≤N≤100,1≤M≤100)。网格中的每个单元或是干的或是被淹没的,且恰有K个单元被水淹没,(1≤K≤N*M)。正如人们所希望的,湖泊是一个中间单元,它与其他的单元共享一条长边(不是角落)。任何与中间单元共享一条长边或者与连通单元共享一条长边的单元是一个连通单元,是湖泊的一部分。
# 输入
有多组数据。每组的第1行有3个整数N,M和K。第2行到第K+1行,是整数R和C,表示被淹没的位置。
# 输出
对每组测试数据,输出有最大湖泊的单元的数目。
# 样例输入 复制
3 4 5 3 2 2 2 3 1 2 3 1 1# 样例输出 复制
4
# 思路:
相当经典的一道DFS题目,我们就从每个湖泊上下左右地去搜索就好了。
下方的代码是非常标准的DFS,读者一定要认真学习~
我们的思路是找到最大的湖泊,我们假设用数组存储这个图,最大的湖泊就是被我们标注为1最多的地方。
我们就从一个湖泊点开始,上下左右地寻找其他湖泊格子,找到1个就加1,如果是越界、发现不是湖泊格子就加0。
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int mx[1001][1001];
int n,m,k;
int dfs(int x,int y){
if(x == 0 || y == 0 || x == n + 1 || y == m + 1 || mx[x][y] == 0) return 0;
if(mx[x][y]){
mx[x][y] = 0;
return 1 + dfs(x - 1,y) + dfs(x + 1,y) + dfs(x,y + 1) + dfs(x,y - 1);
}
}
int main(){
while(cin >> n >> m >> k){
int r,c;
memset(mx,0,sizeof(mx));
for(int i = 2;i <= k + 1;i++){
cin >> r >> c;
mx[r][c] = 1;
}
int maxx = 0;// 记录最大值
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if(mx[i][j]){
int cnt = dfs(i,j);
maxx = max(cnt,maxx);
}
}
}
cout << maxx << "\n";
}
}
# E003 信道分配 (opens new window)
# 题目描述
当无线电台在一个非常大的区域上传播信号时,为了每个接收器都能得到较强信号,使用转发器转发信号。然而,需要仔细地选择每个转发器使用的频道,以使附近的转发器不彼此干扰。如果邻近的转发器使用不同的频道,条件就得到满足。 因为无线电波的频谱是宝贵的资源,转发器所需频道的数量应减到最少。编程任务:读取转发器网络的描述信息,并计算出所需频道的最小使用量。
# 输入
输入包含许多转发器网络图。每幅图的第一行是转发器数目(1~26)。转发器用连续的大写字母表示,从A开始。例如,10个转发器的名称分别是A,B,C,…,I和J。当转发器的个数是0时,表示输入结束。 转发器数目之后,是其邻近关系的列表。每行的格式为 A:BCDH 表示转发器B、C、D和H与转发器A邻近。第一行描述与转发器A邻近的,第二行描述与B邻近的,直到描述完所有的转发器。如果某个转发器不与其他转发器相邻,它的形式为 A: 转发器依字母顺序列出。 注意:相邻是对称的关系;如果A与B相邻,那么B与A也相邻。因为转发器位于水平面内,由相邻的转发器构成的网络图没有相交的线。
# 输出
对于每幅图(除了最后一个没有转发器),输出一行,是转发器不互相干扰所需的最少频道数。输出格式参考样例输出。注意:频道数为1的话,“channel”为单数。
# 思路:
首先我们要能读懂题目。
这道题的含义是,有很多个地区,我们可以叫做ABCD,然后给每个地区分配一个频道,但是相邻的地区不能是相同的频道。
如果学习过四色猜想(四色定理)【读者如果听了课的话】,就能知道,我们最多需要4个频道,就可以让每个地区的频道都不会和邻居地区们的相同。【就好像地图可以只用4个颜色来表示,而不会出现有两个相邻的地区是同种颜色一样】
这个读入是类似于邻接表的结构,也就是每一行开头的第一个是一个点,然后后面跟着他的各个邻居点。
那我们现在知道最多用4个频道就能解决问题,所以我们就得分类讨论,看看什么时候是1个、2个、3个、4个频道。
如果想要只有1个频道的话,那说明完全没有任何点相邻【读者可以自己想想,如果有点相邻,那这两个点就不能是同个频道,那就至少有2个频道才是】,所以这个特判很好判断。
重点是如何判断有2、3、4个频道呢?
我们还是去搜索!还记得笔者前面提到的,搜索的入门就是枚举所有情况。我们把每个点是什么频道都枚举一次其实就能解决问题。
我们存图这部分不详细讲,简单来说就是把这些点ABCD变成数字1234,然后用二维数组存储他们之间的关系,如果有边,就是1,否则就是0。【记得清空数组】
DFS的部分是核心和重点,我们每次假设有colors种频道,然后看看能不能枚举到一种合法情况。
我们给当前在关注的点分配一种频道,然后我们在去看看他的邻居点是否都能满足、不冲突,如果冲突,我们就再换一种频道试试。
为了防止判断重复、走一些重复的老路,我们每次找的邻居点都从比这个点小的那些点里找。
如果我们一路从点1走到点n,也就是一路从第一个点到最后一个点都枚举完成,并且没有出现任何问题在中途的那些点中。
具体请看代码~
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int n;
int mx[100][100];
int color[100];
// 当前枚举到u点,假设总共有colors种频道
int dfs(int u,int colors){
for(int i = 1;i <= colors;i++){
int flag = 1; // flag为1就是假设当前这个频道i是成立的
color[u] = i; // 假设u点的频道是i
for(int v = 1;v < u;v++){
// 如果v点相邻且频道相同,说明这条路走不通
if(mx[u][v] && color[u] == color[v]){
flag = 0; // u的这个频道不成立
break;
}
}
// 如果这条路没遇到问题,并且我们已经在最后一段路
// 或者说
// 如果我们 从来 没遇到问题,同时已经遍历到最后一个点的情况
// 那么我们就已经找到了答案
if(flag && (u == n || dfs(u + 1,colors))){
// 这里的或运算||代表着,如果我们其中有一个点不满足就不成立,必须都满足才成立
return true;
}
}
return false;
}
int main(){
while(cin >> n){
if(!n) break;
memset(mx,0,sizeof(mx));
memset(color,0,sizeof(color));
string s;
int flag = 0; // flag为0说明没有任何邻居点
for(int i = 1;i <= n;i++){
cin >> s;
int u = s[0] - 'A' + 1;
for(int j = 2;j < s.size();j++){
flag = 1; // 说明存在邻居点
int v = s[j] - 'A' + 1;
mx[u][v] = mx[v][u] = 1;
}
}
if(!flag){
cout << "1 channel needed.\n";
}else if(dfs(1,2)){
cout << "2 channels needed.\n";
}else if(dfs(1,3)){
cout << "3 channels needed.\n";
}else{
cout << "4 channels needed.\n";
}
}
}
# E004 移动的骑士 (opens new window)
# 题目描述
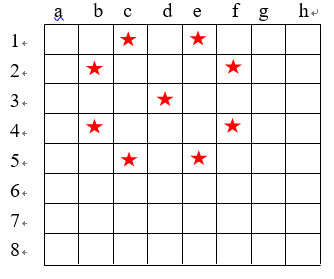
你的一个朋友正在研究骑士旅行问题(TKP)。在一个有n个方格的棋盘上,你得找到一条最短的封闭骑士旅行的路径,使能够遍历每个方格一次。他认为问题的最困难部分在于,对两个给定的方格,确定骑士移动所需的最小步数。所以你帮助他编写一个程序,解决这个“困难的”部分。你的任务是:输入有两个方格a和b,确定骑士在最短路径上从a到b移动的次数。
国际象棋中的骑士在棋盘上可移动的范围如下图:
# 输入
输入包含一组或多组测试例。每个测试例一行,是两个方格,用空格隔开。棋盘上的一个方格用一个字符串表示,字母(a-h)表示列,数字(1-8)表示行。
# 输出
对每个测试例,输出一行:“To get from xx to yy takes n knight moves.”。
# 样例输入 复制
e2 e4 a1 b2 b2 c3 a1 h8 a1 h7 h8 a1 b1 c3 f6 f6# 样例输出 复制
To get from e2 to e4 takes 2 knight moves. To get from a1 to b2 takes 4 knight moves. To get from b2 to c3 takes 2 knight moves. To get from a1 to h8 takes 6 knight moves. To get from a1 to h7 takes 5 knight moves. To get from h8 to a1 takes 6 knight moves. To get from b1 to c3 takes 1 knight moves. To get from f6 to f6 takes 0 knight moves.
# 思路:
这道题是,最搜索的一道题了,符合搜索的本意【?】
DFS:
我们要找到从a点到b点的一条路,或者也不需要知道这条路,我们只要记录从a点到b点要走几步就好。
我的一个基本思路就是,类似于上面的闪避湖泊,我们就从起点a开始,往八个方向去寻找,看看能不能遇到我们要的目的地b。
所以我们就会写出下面的代码,去记录我们走到哪里了(x和y)和我们走了几步(move)
void dfs(int x,int y,int move){ dfs(x - 1,y - 2,move + 1); dfs(x - 1,y + 2,move + 1); dfs(x + 1,y - 2,move + 1); dfs(x + 1,y + 2,move + 1); dfs(x + 2,y - 1,move + 1); dfs(x - 2,y - 1,move + 1); dfs(x + 2,y + 1,move + 1); dfs(x - 2,y + 1,move + 1); }但是我们这个递归什么时候结束?我们的搜索要有结束条件,比如我们跑出了这个8 * 8的格子,所以我们继续完善:
void dfs(int x,int y,int move){ // 非法情况 if(x <= 0 || y <= 0 || x > 8 || y > 8){ return ; } dfs(x - 1,y - 2,move + 1); dfs(x - 1,y + 2,move + 1); dfs(x + 1,y - 2,move + 1); dfs(x + 1,y + 2,move + 1); dfs(x + 2,y - 1,move + 1); dfs(x - 2,y - 1,move + 1); dfs(x + 2,y + 1,move + 1); dfs(x - 2,y + 1,move + 1); }那我们什么时候可以找到答案呢,就是当x和y走到b点的时候。我们可以用一个变量去记录我们要的答案,所以我们可以用全局变量ans去获取。
int ans = INF; // 我这边定义INF = 0x3f3f3f3f,其实就是一个足够大的数字而已 void dfs(int x,int y,int move){ // 到达了 if(x == xx2 && y == yy2){ ans = min(ans,move); return ; } // 非法情况 if(x <= 0 || y <= 0 || x > 8 || y > 8){ return ; } dfs(x - 1,y - 2,move + 1); dfs(x - 1,y + 2,move + 1); dfs(x + 1,y - 2,move + 1); dfs(x + 1,y + 2,move + 1); dfs(x + 2,y - 1,move + 1); dfs(x - 2,y - 1,move + 1); dfs(x + 2,y + 1,move + 1); dfs(x - 2,y + 1,move + 1); }但是这个程序没办法真的这么走,因为如果想要走完所有情况,那我们计算机内存都爆炸了,因为你会在几个点之间打转,不可能结束的,所以笔者在这里限制了搜索的步数(不能超过7步)就会得到下方的错解。【错解是因为要是有的答案需要超过七步才能得到的话,那我们就肯定错了。但是因为OJ数据比较水,所以就通过啦~】
那我们刚刚这个思路不太好怎么办?我们其实可以想办法记录结果。
我们可以用个mx数组记录每个格子到达时的步数,并且取更小的一个。
这样就不会出现在几个点打转的情况了【读者自行思考为什么】
if(move >= mx[x][y]) return ; mx[x][y] = move;以上就是DFS版本的完整思路。
如果读者学习过BFS,这道题更加容易,因为其实这类寻找最少步数、最优解、最好情况、最短路径的问题,都应该用BFS解决会容易,这是广搜的优越性。
读者可以自行撰写BFS版本的代码,这里不阐述BFS的思路。下方笔者给出了一版BFS的写法,读者可以参考学习。
# 代码C++ 可以通过但其实是错的解:
#include<bits/stdc++.h>
using namespace std;
int xx1,xx2,yy1,yy2;
const int INF = 0x3f3f3f3f;
int ans = INF; // ans记录移动了几步
// move表示此时已经移动了几步,x和y表示移动到了哪里
void dfs(int x,int y,int move){
if(move > 7) return ; // 错误,但我们可以假设我们找七次,找不到就算了
// 到达了
if(x == xx2 && y == yy2){
ans = min(ans,move);
return ;
}
// 非法情况
if(x <= 0 || y <= 0 || x > 8 || y > 8){
return ;
}
dfs(x - 1,y - 2,move + 1);
dfs(x - 1,y + 2,move + 1);
dfs(x + 1,y - 2,move + 1);
dfs(x + 1,y + 2,move + 1);
dfs(x + 2,y - 1,move + 1);
dfs(x - 2,y - 1,move + 1);
dfs(x + 2,y + 1,move + 1);
dfs(x - 2,y + 1,move + 1);
}
int main(){
string a,b;
while(cin >> a >> b){
ans = INF;
// 先提取出a点和b点
xx1 = a[0] - 'a' + 1;
yy1 = a[1] - '0';
xx2 = b[0] - 'a' + 1;
yy2 = b[1] - '0';
dfs(xx1,yy1,0);
cout << "To get from " << a << " to " << b << " takes " << ans << " knight moves." << "\n";
}
}
# 代码C++ DFS版本:
#include<bits/stdc++.h>
using namespace std;
int xx1,xx2,yy1,yy2;
int mx[10][10];
// move表示此时已经移动了几步,x和y表示移动到了哪里
void dfs(int x,int y,int move){
// 非法情况
if(x <= 0 || y <= 0 || x > 8 || y > 8){
return ;
}
if(move >= mx[x][y]) return ;
mx[x][y] = move;
dfs(x - 1,y - 2,move + 1);
dfs(x - 1,y + 2,move + 1);
dfs(x + 1,y - 2,move + 1);
dfs(x + 1,y + 2,move + 1);
dfs(x + 2,y - 1,move + 1);
dfs(x - 2,y - 1,move + 1);
dfs(x + 2,y + 1,move + 1);
dfs(x - 2,y + 1,move + 1);
}
int main(){
string a,b;
while(cin >> a >> b){
memset(mx,0x3f,sizeof(mx));
// 先提取出a点和b点
xx1 = a[0] - 'a' + 1;
yy1 = a[1] - '0';
xx2 = b[0] - 'a' + 1;
yy2 = b[1] - '0';
dfs(xx1,yy1,0);
cout << "To get from " << a << " to " << b << " takes " << mx[xx2][yy2] << " knight moves." << "\n";
}
}
# 代码C++ BFS版本:
#include<bits/stdc++.h>
using namespace std;
int xx1,xx2,yy1,yy2;
int mx[10][10]; // 存储每个位置的最小步数
int dx[] = {-1, -1, 1, 1, 2, -2, 2, -2}; // 横向移动
int dy[] = {-2, 2, -2, 2, -1, -1, 1, 1}; // 纵向移动
// 广度优先搜索函数
void bfs(int x, int y) {
queue<pair<int, int>> q; // 队列,用pair可以存储坐标
q.push({x, y});
mx[x][y] = 0; // 起始位置的步数为0
while (!q.empty()) {
pair<int, int> curr = q.front();
q.pop();
int cx = curr.first, cy = curr.second;
int move = mx[cx][cy];
// 遍历8个方向
for (int i = 0; i < 8; i++) {
int nx = cx + dx[i], ny = cy + dy[i];
// 检查新位置是否合法并且未访问过
if (nx > 0 && nx <= 8 && ny > 0 && ny <= 8 && move + 1 < mx[nx][ny]) {
mx[nx][ny] = move + 1;
q.push({nx, ny});
}
}
}
}
int main() {
string a,b;
while (cin >> a >> b) {
memset(mx, 0x3f, sizeof(mx));
xx1 = a[0] - 'a' + 1;
yy1 = a[1] - '0';
xx2 = b[0] - 'a' + 1;
yy2 = b[1] - '0';
// 从起始点开始广度优先搜索
bfs(xx1, yy1);
cout << "To get from " << a << " to " << b << " takes " << mx[xx2][yy2] << " knight moves." << "\n";
}
}
# E005 图像周长 (opens new window)
# 题目描述
病理学实验室的技术人员需要分析幻灯片的数字图像。幻灯片上有许多要分析的目标,由鼠标单击确定一个目标。目标边界的周长是一个有用的测量参数。编程任务:确定选中目标的在周长。 数字化的幻灯片是一个矩形的网格,里面有点’.’,表示空的地方;有大写字母‘X’,表示目标的一部分。简单网格如下所示
方格中的一个X是指一个完整的网络方形区域,包括其边界和目标本身。网格中心的X与其边界上8个方向的X都是相邻的。任何两个相邻的X,其网格方形区域在边界或者拐角处是重叠的,所以他们的网格方形区域是相邻的。 一个目标是由一系列相邻X的网格方形区域连接起来构成的。在网格1中,一个目标填充了全部网格;在网格2中有两个目标,其中一个目标只占左下角的一个网格方形区域,其余的X属于另一个目标。 技术人员总是能单击到一个X,以选中包含该X的目标,记录单击时的坐标。行列号是从左上角开始,从1开始编号的。在网格1中,技术人员可以单击行2和列2选择目标;在网格2中,单击行2和列3就可以选中较大目标,单击行4和列3就不能选中任何目标。 一个有用的统计参数是目标的周长。假定每个X的每条边上有一个方形的单元。在网格1中目标的周长是8(4个边,每个边上有2个方形的单元);在网格2中,较大目标的周长是18,如下图所示。
目标中不会包含任何完全封闭的孔,所以下面最左边的网格不会出现,应该是右边的网格样式。
# 输入
输入有多组网格。对每个网格,第一行是网格的行列数(rows,columns),鼠标单击的行列号(row,column),其整数范围都是1-20.接下来就是rows行,由字符‘.’和‘X’构成。 当一行是4个0时,标志输入结束。一行中的4个数字之间各有一个空格。网格数据的行之间没有空行。
# 输出
对每个网络输出一行,是选中目标的周长。
# 样例输入 复制
2 2 2 2 XX XX 6 4 2 3 .XXX .XXX .XXX ...X ..X. X... 5 6 1 3 .XXXX. X....X ..XX.X .X...X ..XXX. 0 0 0 0# 样例输出 复制
8 18 40
# 思路:
这道题是这样的。
首先给了个起点,所以你可以上下左右斜角(总共8个方向)去搜索,所以这个是容易的。
但是要如何处理外围边界的一圈,这确实是个问题。
这道题做法很多,笔者这里用的是一种相较简单的做法。我们首先将这个图形的周围一圈用 . 覆盖,这样就不会出现特判的情况。
然后我们就正常DFS从起点开始,往八个方向去搜索,并且搜索到的点都要被标记。
所以这样,我们就相当于从图上,把这一个“目标”给“提取”出来了。
在这个过程中,我们把所有遇到的 . 都算进长度里,遇到一个算一个。最后这个周长就算出来了。
用一句话总结就是:从起点开始,我们在X里搜索,遇到的所有 . 都是长度的一部分【因为周长一定是与 . 相邻的部分】。
当然这道题还有很多做法,包括BFS什么的,欢迎读者自行尝试。
# 代码C++ DFS版本:
#include<bits/stdc++.h>
using namespace std;
char mx[100][100];
int len = 0;
int step_8[8][2] = {{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}}; // 周围一圈
int step_4[4][2] = {{-1,0},{1,0},{0,1},{0,-1}}; // 左右上下
void dfs(int x,int y){
// 标记为访问过了
if(mx[x][y] == 'X') mx[x][y] = ' ';
// 把整个目标里的X都遍历
for(int i = 0;i < 8;i++){
int nx = x + step_8[i][0];
int ny = y + step_8[i][1];
if(mx[nx][ny] == 'X') dfs(nx,ny);
}
// 看看这一团目标,能搜到多少个.在四周
for(int i = 0;i < 4;i++){
int nx = x + step_4[i][0];
int ny = y + step_4[i][1];
if(mx[nx][ny] == '.') len++;
}
}
int main(){
int rows,cols,xx,yy;
while(cin >> rows >> cols >> xx >> yy){
if(!rows && !cols && !xx && !yy) break;
len = 0;
// 先把周围一圈包起来
for(int i = 0;i <= cols + 1;i++){
mx[0][i] = '.';
mx[rows + 1][i] = '.';
}
for(int i = 0;i <= rows + 1;i++){
mx[i][0] = '.';
mx[i][cols + 1] = '.';
}
for(int i = 1;i <= rows;i++){
for(int j = 1;j <= cols;j++){
cin >> mx[i][j];
}
}
dfs(xx,yy);
cout << len << "\n";
}
}