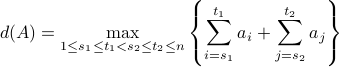# NENUOJ 之 算法2动态规划D
# 前言
这一章是动态规划,理解上可能会比较晦涩,但是还是希望读者能尽量去理解其中的精华。
# D001 数字三角形 (opens new window)
# 题目描述
7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和。
注意:路径上的每一步只能从一个数走到下一层上和它最近的左边的那个数或者右边的那个数。
# 输入
输入的第一行是一个整数N (1 < N <= 100),给出三角形的行数。下面的N行给出数字三角形。数字三角形上的数的范围都在0和100之间。
# 输出
输出最大的和。
# 样例输入 复制
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5# 样例输出 复制
30
# 思路:
动态规划(DP)是分阶段解决问题的方法,适用于需要根据子问题的解来构造整个问题解的情况。
这道题的思路就是整个读入之后,然后从上往下递推【从下往上也不是不行】,然后处理一下边界就行。
我们从三角形的顶部开始,逐步向下计算每个位置可以得到的最大和。
$dp[i][j]$表示从顶部到达位置 $(i, j)$ 的最大和。
我们递推公式就是$dp[i][j] = max(dp[i - 1][j - 1],dp[i - 1][j]) + a[i][j]$,从上一层的两个可能位置选择最大值,并加上当前值。【然后最好处理一下边界值,虽然不处理应该也没事】
其实这种三角形的题目,我们最好采用自下而上的办法,即下方第二部分的代码,公式是$dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j]$, $a[i][j]$是当前位置的数字,$dp[i+1][j]$ 和 $dp[i+1][j+1]$ 是下一行的两个可能的选择。我们选择其中较大的一个,再加上当前位置的数字,即可得到当前位置的最大和。
剩下读者自行理解~
# 代码C++ 自顶向下版:
#include<bits/stdc++.h>
using namespace std;
int a[1005][1005];
int dp[1005][1005];
int main(){
int n;
int maxx = -1;
while(cin >> n){
maxx = -1;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= i;j++){
cin >> a[i][j];
dp[i][j] = a[i][j];
}
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= i;j++){
if(i - 1 >= 1 && j - 1 >= 1)
dp[i][j] = max(dp[i - 1][j - 1],dp[i - 1][j]) + a[i][j];
else if(j - 1 == 0)
dp[i][j] = dp[i - 1][j] + a[i][j];
maxx = max(dp[i][j],maxx);
}
}
cout << maxx << "\n";
}
}
# 代码C++ 自底向上版本:
#include<bits/stdc++.h>
using namespace std;
int a[1005][1005];
int dp[1005][1005];
int main(){
int n;
int maxx = -1;
while(cin >> n){
maxx = -1;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= i;j++){
cin >> a[i][j];
dp[i][j] = a[i][j];
}
}
// 从倒数第二行开始,计算每个位置的最大路径和
for(int i = n - 1;i >= 1;i--){
for(int j = 1;j <= i;j++){
dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + a[i][j];
maxx = max(dp[i][j], maxx);
}
}
cout << maxx << "\n";
}
}
# D002 最长上升子序列 (opens new window)
# 题目描述
一个数的序列bi,当b1 < b2 < ... < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, ..., aN),我们可以得到一些上升的子序列(ai1, ai2, ..., aiK),这里1 <= i1 < i2 < ... <iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8)。
你的任务,就是对于给定的序列,求出最长上升子序列的长度。
# 输入
输入有很多组,每组输入的第一行是序列的长度N (1 <= N <= 1000)。第二行给出序列中的N个整数,这些整数的取值范围都在0到10000。
# 输出
输出每组的最长上升子序列的长度。
# 样例输入 复制
7 1 7 3 5 9 4 8 6 2 3 4 1 6 5# 样例输出 复制
4 4
# 思路:
经典之中的经典题,必会!
其实就是一种暴力,但是又用数组保存了【到当前索引最长的上升长度】这个事情。
对于每个元素 $a[i]$,我们查找其之前所有的元素$a[j]$($j < i$),如果$a[i] > a[j]$,则说明可以将 $a[i]$ 加到以 $a[j]$ 为结尾的上升子序列中,此时 $dp[i] = max(dp[i], dp[j] + 1)$ ,即长度 + 1。
最后我们直接输出最大的一个dp值【即找到一个最长的结尾值】【但是OJ不加这一段都行,数据太弱了,所以会导致一些错误代码通过】
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int a[10000];
int dp[1005];
int main(){
int n;
while(cin >> n){
for(int i = 1;i <= n;i++){
cin >> a[i];
dp[i] = 1;
}
for(int i = 1;i <= n;i++){
for(int j = 1;j < i;j++){
if(a[i] > a[j]){
dp[i] = max(dp[i],dp[j] + 1);
}
}
}
// 输出最大的一个dp值
int maxx = -1;
for(int i = 1;i <= n;i++){
maxx = max(maxx,dp[i]);
}
cout << maxx << "\n";
}
}
# D003 Help Jimmy (opens new window)
# 题目描述
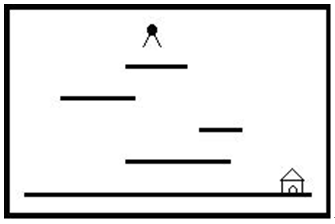
"Help Jimmy" 是在下图所示的场景上完成的游戏:
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。 Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。 设计一个程序,计算Jimmy到地面时可能的最早时间。
# 输入
第一行是测试数据的组数t(0 <= t <= 20)。每组测试数据的第一行是四个整数N,X,Y,MAX,用空格分隔。N是平台的数目(不包括地面),X和Y是Jimmy开始下落的位置的横竖坐标,MAX是一次下落的最大高度。接下来的N行每行描述一个平台,包括三个整数,X1[i],X2[i]和H[i]。H[i]表示平台的高度,X1[i]和X2[i]表示平台左右端点的横坐标。1<= N <= 1000,-20000 <= X, X1[i], X2[i] <= 20000,0 < H[i] < Y <= 20000(i = 1..N)。所有坐标的单位都是米。 Jimmy 的大小和平台的厚度均忽略不计。如果Jimmy 恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保Jimmy一定能安全到达地面。
# 输出
对输入的每组测试数据,输出一个整数,Jimmy到地面时可能的最早时间。
# 样例输入 复制
1 3 8 17 20 0 10 8 0 10 13 4 14 3# 样例输出 复制
23
# 思路:
这道题有点复杂,其实是这样处理的。我们把地面也当作一个无限大的平台,然后把所有平台进行排序。
之后我们对在平台上向左还是向右的情况进行分类讨论,然后再对能否落到平台这件事再分类讨论。
有点复杂,直接看代码吧,我们用二维dp数组记录向左/向右的落地最短时间。
这道题我们用flat结构体记录左端点、右端点、高度,然后我们就去模拟一个人如果向左想要到下一块板子,那左端点就得在下一块板子的左右之间,同理,如果一个人想要向右到达下一块板子,那右端点就得在下一块板子的左右之间。
我们的dp数组有两维,第一维记录向左(0)跑或者向右(1)跑,第二维记录在哪一块板子上。
既然我们有第一块板子、第二块板子这样的区分,我们就肯定需要把这些板子进行排序~
然后我们写两个函数,分别对应left和right。
我们分析一下left(向左端点跑)的情况,首先我们用while循环去找(向左端点跑)能到的板子【不是下一块板子i - 1就一定是哦】,我们需要去判断:我们要去的下一块板子是否能接住、我们要去的下一块板子是否高度会超过。第一个条件好判断,我们用$a[temp].l <= a[i].l \space&&\space a[i].l <= a[temp].r$ 【temp是我们正在判断能不能去的下一块板子】即可判断,第二个条件也很好判断,但是我们还要用dp数组记录时间。
下降时间很好判断,即 $a[i].h - a[temp].h$ ,但我们也要算移动时间,我们用$min(dp[temp][0] + a[i].l-a[temp].l,dp[temp][1] + a[temp].r-a[i].l)$ 记录,$a[i].l - a[temp].l$ 即为要跑到下一个板子的左端点,还是$a[temp].r-a[i].l$跑到下一个板子的右端点,这里出现的dp其实有点难理解,但是因为我们其实最后循环是自下而上推导的,所以我们这个时候dp记录的是第temp板子与地面之间的时间,然后加上刚刚我们算的这两块板之间的时间,这些共同组成了所有的时间。
最后我们自底向上进行时间计算,依次计算假设我们从第2块板开始下降、第3块板开始下降、第4块板开始下降…第n + 1块板开始下降,输出 $min(dp[n+1][0],dp[n+1][1])$ 即为我们从第n + 1块板开始下降的最短时间了。
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 5;
int dp[2005][2];
int n,x,y,maxx;
typedef struct flat{
int l = 0;
int r = 0;
int h = 0;
}flat;
flat a[1005];
bool cmp(flat a,flat b){
return a.h < b.h;
}
void left(int i){
int temp = i - 1;
while(temp > 0 && a[i].h - a[temp].h <= maxx){
if(a[temp].l <= a[i].l && a[i].l <= a[temp].r){ // 一定会落到板子上
dp[i][0] = (a[i].h - a[temp].h) + min(dp[temp][0] + a[i].l-a[temp].l,dp[temp][1] + a[temp].r-a[i].l);
return;
}
temp--;
}
if(a[i].h - a[temp].h > maxx){
dp[i][0] = MAXN;
}else{
dp[i][0] = a[i].h;
}
}
void right(int i){
int temp = i - 1;
while(temp > 0 && a[i].h - a[temp].h <= maxx){
if(a[temp].l <= a[i].r && a[i].r <= a[temp].r){ // 一定会落到板子上
dp[i][1] = (a[i].h - a[temp].h) + min(dp[temp][0] + a[i].r-a[temp].l,dp[temp][1] + a[temp].r-a[i].r);
return;
}
temp--;
}
if(a[i].h - a[temp].h > maxx){
dp[i][1] = MAXN;
}else{
dp[i][1] = a[i].h;
}
}
void solve(){
cin >> n;
cin >> a[n + 1].l >> a[n + 1].h >> maxx;
for(int i = 1;i <= n;i++){
cin >> a[i].l >> a[i].r >> a[i].h;
}
//起点
a[n + 1].r = a[n + 1].l;
//平台
a[0].l = -MAXN;
a[0].r = MAXN;
a[0].h = 0;
sort(a,a + n + 1,cmp);
for(int i = 1;i <= n + 1;++i){
left(i);
right(i);
}
cout << min(dp[n+1][0],dp[n+1][1]) << "\n";
}
int main(){
int t;
cin >> t;
while(t--) solve();
}
# D004 最长公共子序列 (opens new window)
# 题目描述
我们称序列Z = < z1, z2, ..., zk >是序列X = < x1, x2, ..., xm >的子序列当且仅当存在严格上升的序列< i1, i2, ..., ik >,使得对j = 1, 2, ... ,k, 有xij = zj。比如Z = < a, b, f, c > 是X = < a, b,c, f, b, c >的子序列。 现在给出两个序列X和Y,你的任务是找到X和Y的最大公共子序列,也就是说要找到一个最长的序列Z,使得Z既是X的子序列也是Y的子序列。
# 输入
输入包括多组测试数据。每组数据包括一行,给出两个长度不超过200的字符串,表示两个序列。两个字符串之间由若干个空格隔开。
# 输出
对每组输入数据,输出一行,给出两个序列的最大公共子序列的长度。
# 样例输入 复制
abcfbc abfcab programming contest abcd mnp# 样例输出 复制
4 2 0
# 思路:
这道题也是经典题目~
其实就是分类讨论+暴力双循,如果当前点符合,长度就是【之前状态+1】,如果不符合,当前状态就等于max(【之前状态】)。
首先搞清楚题意,也就是我们要在两个字符串中,找到最长的那个公共的子序列。
我们用二维dp数组记录两个事情,一维记录字符串1,二维记录字符串2,$dp[i][j]$ 即为,当计算到字符串1的第$i$个和字符串2的第$j$个的位置时,此时找到的最长的公共子序列有多长。
如果字符相等($a[i-1] == b[j-1]$):如果 $a[i-1]$ 和 $b[j-1]$ 相同,意味着这两个字符可以作为公共子序列的一部分。因此,$dp[i][j]$ 应该等于 $dp[i-1][j-1] + 1$,即继承自前一个子问题的解,并加上当前字符。
如果字符不相等:如果 $a[i-1]$和 $b[j-1]$ 不相同,最长公共子序列应该是忽略其中一个字符后的最大公共子序列长度,即:$dp[i][j] = max(dp[i-1][j], dp[i][j-1])$,选择从 $a$ 中剔除一个字符(即 $dp[i-1][j]$),或者从 $b$ 中剔除一个字符(即 $dp[i][j-1]$),取两者中的最大值。
简而言之:如果相等,那么当前的公共子序列长度就是前一个子问题的长度加一 $dp[i][j] = dp[i - 1][j - 1] + 1$;如果不相等,当前的公共子序列长度就是前面两个子问题的最大值 $dp[i][j] = max(dp[i][j - 1],dp[i - 1][j])$。
# 代码C++ dp部分展开:
#include<bits/stdc++.h>
using namespace std;
const int MAXX = 1e3;
int dp[MAXX][MAXX];
int len1;
int len2;
void solve(string a,string b){
len1 = a.size();
len2 = b.size();
for(int i = 0;i < len1;i++){
for(int j = 0;j < len2;j++){
dp[i][j] = 0;
}
}
for(int i = 1;i <= len1;i++){
for(int j = 1;j <= len2;j++){
if(a[i - 1] == b[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
} else if(dp[i - 1][j] > dp[i][j - 1]){
dp[i][j] = dp[i - 1][j];
} else{
dp[i][j] = dp[i][j - 1];
}
}
}
cout << dp[len1][len2] << "\n";
}
int main(){
string a,b;
while(cin >> a >> b){
solve(a,b);
}
}
# 代码C++ dp部分不展开:
#include<bits/stdc++.h>
using namespace std;
const int MAXX = 1e3;
int dp[MAXX][MAXX];
int len1;
int len2;
void solve(string a,string b){
len1 = a.size();
len2 = b.size();
for(int i = 0;i < len1;i++){
for(int j = 0;j < len2;j++){
dp[i][j] = 0;
}
}
for(int i = 1;i <= len1;i++){
for(int j = 1;j <= len2;j++){
if(a[i - 1] == b[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = max(dp[i][j - 1],dp[i - 1][j]);
}
}
}
cout << dp[len1][len2] << "\n";
}
int main(){
string a,b;
while(cin >> a >> b){
solve(a,b);
}
}
# D005 陪审团的人选 (opens new window)
# 题目描述
在遥远的国家佛罗布尼亚,嫌犯是否有罪,须由陪审团决定。陪审团是由法官从公众中挑选的。先随机挑选n个人作为陪审团的候选人,然后再从这n个人中选m人组成陪审团。选m人的办法是: 控方和辩方会根据对候选人的喜欢程度,给所有候选人打分,分值从0到20。为了公平起见,法官选出陪审团的原则是:选出的m个人,必须满足辩方总分和控方总分的差的绝对值最小。如果有多种选择方案的辩方总分和控方总分的之差的绝对值相同,那么选辩控双方总分之和最大的方案即可。最终选出的方案称为陪审团方案。
# 输入
输入包含多组数据。每组数据的第一行是两个整数n和m,n是候选人数目,m是陪审团人数。注意,1<=n<=200, 1<=m<=20而且m<=n。接下来的n行,每行表示一个候选人的信息,它包含2个整数,先后是控方和辩方对该候选人的打分。候选人按出现的先后从1开始编号。两组有效数据之间以空行分隔。最后一组数据n=m=0。
# 输出
对每组数据,先输出一行,表示答案所属的组号, 如 'Jury #1', 'Jury #2', 等。接下来的一行要象例子那样输出陪审团的控方总分和辩方总分。再下来一行要以升序输出陪审团里每个成员的编号,两个成员编号之间用空格分隔。每组输出数据须以一个空行结束。
# 样例输入 复制
4 2 1 2 2 3 4 1 6 2 0 0# 样例输出 复制
Jury #1 Best jury has value 6 for prosecution and value 4 for defence: 2 3
# 思路:
这题难读且难写,推荐跳过【。】。但是其实就是个01背包,每个人要么被选择要么不被选择。
思路请参考:POJ 1015 Jury Compromise (完全背包) - RioTian - 博客园 (cnblogs.com) (opens new window)
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
const int OFFSET = 400;
const int MAX_DIFF = 800;
const int MAX_N = 205;
const int MAX_M = 25;
int f[MAX_M][MAX_DIFF + 1]; // 动态规划表
int d[MAX_N][MAX_M][MAX_DIFF + 1]; // 路径记录
int n, m, a[MAX_N], b[MAX_N], suma, sumb, T;
vector<int> c;
void get_path(int i, int j, int k) {
if (j == 0) return;
int last = d[i][j][k];
get_path(last - 1, j - 1, k - (a[last] - b[last]));
c.push_back(last);
suma += a[last];
sumb += b[last];
}
int main() {
T = 1;
while (true) {
cin >> n >> m;
if (n == 0 && m == 0) break;
// 读入候选人的控方和辩方分数
for (int i = 1; i <= n; ++i) {
cin >> a[i] >> b[i];
}
// 初始化动态规划表
memset(f, -0x3f, sizeof(f)); // -INF
f[0][OFFSET] = 0; // 平移到 OFFSET
// 动态规划过程
for (int i = 1; i <= n; ++i) {
// 不选择第 i 个人
for (int j = 0; j <= m; ++j) {
for (int k = 0; k <= MAX_DIFF; ++k) {
d[i][j][k] = d[i - 1][j][k];
}
}
// 选择第 i 个人
for (int j = m; j > 0; --j) {
for (int k = 0; k <= MAX_DIFF; ++k) {
int diff = a[i] - b[i];
if (k - diff < 0 || k - diff > MAX_DIFF) continue; // 超出范围
if (f[j][k] < f[j - 1][k - diff] + a[i] + b[i]) {
f[j][k] = f[j - 1][k - diff] + a[i] + b[i];
d[i][j][k] = i;
}
}
}
}
// 寻找最佳解
int ans = 0;
for (int k = 0; k <= OFFSET; ++k) {
if (f[m][OFFSET + k] >= 0 && f[m][OFFSET + k] >= f[m][OFFSET - k]) {
ans = k + OFFSET;
break;
}
if (f[m][OFFSET - k] >= 0) {
ans = OFFSET - k;
break;
}
}
// 恢复路径
c.clear();
suma = sumb = 0;
get_path(n, m, ans);
// 输出
cout << "Jury #" << T++ << endl;
cout << "Best jury has value " << suma << " for prosecution and value " << sumb << " for defence:" << "\n";
for (size_t i = 0; i < c.size(); ++i) {
if (i > 0) cout << " ";
cout << c[i];
}
cout << "\n\n";
}
return 0;
}
# D006 最大和 (opens new window)
# 题目描述
给定一个n个整数的集合:A={a1, a2,..., an},我们如下定义函数d(A):
你的任务就是计算函数d(A)的函数值。 提示:对于样例,我们选择{2,2,3,-3,4} 和 {5},进行想加得到函数d(A)的函数值。 输入量大,建议使用scanf();
# 输入
输入包含 T(<=30)个样例,在输入的第一行即是整数T。每个样例包含两行,第一行是整数 n(2<=n<=50000),第二行包含了n个整数: a1, a2, ..., an. (|ai| <= 10000)。
# 输出
对于每个输入样例,输出一行,即如上定义函数d(A)的函数值。
# 样例输入 复制
1 10 1 -1 2 2 3 -3 4 -4 5 -5# 样例输出 复制
13
# 思路:
这道题其实就是找一个临界点,合并一个最大的前缀子数组和+最大的后缀子数组和。
如果能想明白这件事,那这道题就不难了,也就是前后两次扫描,然后类似于求最大的子数组和这件事去处理,最后再拼接起来。
即寻找两个不相交子数组的最大和。
# 代码C++ 第一版:
#include<bits/stdc++.h>
using namespace std;
const int MAXX = 2e5;
const int INF = 0x3f3f3f3f;
int a[MAXX];
int dp1[MAXX];
int dp2[MAXX];
int maxx;
void solve(){
int n;
cin >> n;
for(int i = 1;i <= n;i++){
cin >> a[i];
dp1[i] = 0;
dp2[i] = 0;
maxx = 0;
}
dp1[0] = -INF;
int sum = 0;
for(int i = 1;i <= n;i++){
dp1[i] = max(dp1[i - 1],sum + a[i]);
sum += a[i];
if(sum < 0){
sum = 0;
}
}
dp2[n + 1] = -INF;
sum = 0;
for(int i = n;i > 0;i--){
dp2[i] = max(dp2[i + 1],sum + a[i]);
sum += a[i];
if(sum < 0){
sum = 0;
}
}
int res = -INF;
for(int i = n;i > 0;i--){
res = max(res,dp1[i] + dp2[i + 1]);
}
cout << res << "\n";
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--) solve();
}
# 代码C++ 第二版:
#include <bits/stdc++.h>
using namespace std;
const int MAXX = 2e5;
const int INF = 0x3f3f3f3f;
int a[MAXX];
int dp1[MAXX];
int dp2[MAXX];
void solve(){
int n;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
int sum = 0;
dp1[0] = -INF;
for(int i = 1; i <= n; i++){
dp1[i] = max(dp1[i - 1], sum + a[i]);
sum = max(0, sum + a[i]);
}
sum = 0;
dp2[n + 1] = -INF;
for(int i = n; i > 0; i--){
dp2[i] = max(dp2[i + 1], sum + a[i]);
sum = max(0, sum + a[i]);
}
int res = -INF;
for(int i = 1; i < n; i++){
res = max(res, dp1[i] + dp2[i + 1]);
}
cout << res << "\n";
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--) solve();
}
# D007 最大子矩阵 (opens new window)
# 题目描述
给你一个二维矩阵,元素是整数,有正有负。一个子矩阵就是最小1*1最大包含这个矩阵本身的矩阵。一个矩阵的和就是矩阵中所有元素求和,最大子矩阵就是所有子矩阵中和最大的那个字矩阵。下面是一个例子: 0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2 最大子矩阵在左下角 9 2 -4 1 -1 8 和值是15。
# 输入
输入的第一行是整数N,即表示要输入一个N * N的整数矩阵。接下来是N^2 个整数,每个整数之间被空格或者空行分开,这些整数即为矩阵中的数,按照列优先的顺序排列,即第一行整数从左至右输入,第二行从左至右输入…. 第n行从左至右输入。N不会大于100,矩阵中的整数范围为 [-127,127]。
# 输出
输出最大矩阵的和。
# 样例输入 复制
4 0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2# 样例输出 复制
15
# 思路:
这题其实是求最大子段和的延申题目,但是OJ上没有这个前置题目。
最大子段和就是求一行数字里,某一段数字的和是最大的。那个问题的转移方程就是:$b[j]=max({b[j-1]+a[j], a[j]})$
$b[j]$ 是存储最大和,$a[j]$ 是原数组。
然后现在我们把这个最大子矩阵的问题压缩一下,也就是n个最大子矩阵问题。【直接看代码吧】
然后笔者发现这道题在OJ上,不论是暴力还是动态规划的写法都能通过,读者可以自行抉择。【其实暴力不应该能通过才是】
# 代码C++ 暴力版:
#include<bits/stdc++.h>
using namespace std;
int mx[100][100];
int main() {
int n;
cin >> n;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
cin >> mx[i][j];
int maxSum = INT_MIN;
for(int i = 0; i < n; i++) {
for(int j = i; j < n; j++) {
for(int k = 0; k < n; k++) {
for(int l = k; l < n; l++) {
int sum = 0;
for(int p = i; p <= j; p++) {
for(int q = k; q <= l; q++) {
sum += mx[p][q];
}
}
maxSum = max(maxSum, sum);
}
}
}
}
cout << maxSum << "\n";
return 0;
}
# 代码C++ 动态规划版:
#include <bits/stdc++.h>
using namespace std;
int mx[100][100];
int temp[100];
int dp[100];
int maxx = -0x3f3f3f3f;
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> mx[i][j];
}
}
for (int i = 0; i < n; i++) {
memset(temp, 0, sizeof(temp));
for (int j = i; j < n; j++) {
// 更新temp数组
for (int k = 0; k < n; k++) {
temp[k] += mx[j][k];
}
// 求最大子段和
int sum = 0;
for (int k = 0; k < n; k++) {
if (sum > 0) {
sum += temp[k];
} else {
sum = temp[k];
}
maxx = max(maxx, sum);
}
}
}
cout << maxx << "\n";
return 0;
}