# NENUOJ 之 算法2查找C
# 前言
这套题的核心其实就是二分~
虽然我们可以用一些好用的数据结构偷偷懒,但是二分还是得会的!
# C001 字符串计数 (opens new window)
# 题目描述
给出m个字符串,要求输出重复n次的字符串有几个。
# 输入
先给定一个N,N≤100000,接着输入N个字符串。
# 输出
对于每组测试数据,输出若干行,每行两个正整数,第一个数表示重复的次数,第二个数表示在此重复次数下有几种不同的字符串。
# 样例输入 复制
5 BBA BBA BEA DEC CCF# 样例输出 复制
1 3 2 1
# 思路:
这题我看网上的写法都好复杂……笔者这里用map和set使代码长度大大降低!【理解难度++】其实就是用map去记录不同字符串的出现次数和用set的去重以及排序的能力去记录有哪些出现次数。然后就是按照set里那些出现次数【对应的第一个输出】去map里找相同出现次数的字符串有几个【用map的第二项找第一项的个数】【对应第二个输出】。
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
map<string,int> mp; // 记录每个字符串出现几次
set<int> st; // 记录有几种出现次数
int main(){
int n;
cin >> n;
for(int i = 1;i <= n;i++){
string s;
cin >> s;
mp[s]++;
}
for(auto &it : mp){
st.insert(it.second);
}
for(auto it : st){
cout << it << " ";
int cnt = 0;
for(auto &i : mp){
if(i.second == it){
cnt++;
}
}
cout << cnt << "\n";
}
}
# C002 赌徒 (opens new window)
# 题目描述
N个赌徒一起决定玩一个游戏: 游戏刚开始的时候,每个赌徒把赌注放在桌上并遮住,侍者要查看每个人的赌注并确保每个人的赌注都不一样。如果一个赌徒没钱了,则他要借一些筹码,因此他的赌注为负数。假定赌注都是整数。 最后赌徒们揭开盖子,出示他们的赌注。如果谁下的赌注是其他赌徒中某3个人下的赌注之和,则他是胜利者。如果有多于一个胜利者,则下的赌注最大的赌徒才是最终的胜利者。 例如,假定赌徒为:Tom、Bill、John、Roger和Bush,他们下的赌注分别为:2、3、5、7和12 。因此最终获胜的是Bush(并且没有其他人是胜利者),因为他下的赌注为12,而其他的人下的赌注之和也等于12:2+3+7=12。
# 输入
输入文件中包含了多组赌徒下的赌注。每组赌注的数据第1行是一个整数n,1<=n<=1000,代表赌徒的个数,然后是他们下的赌注,每个人的赌注占一行,这些赌注各不相同,并且范围是[-536870912,+536870911]。输入文件的最后一行为0,代表输入结束。
# 输出
对每组赌注,输出胜利者下的赌注,如果没有解,则输出“no solution”。
# 样例输入 复制
5 2 3 5 7 12 5 2 16 64 256 1024 0# 样例输出 复制
12 no solution
# 思路:
这道题其实就是暴力!大胆四层循环就能过~
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int a[10000];
int main(){
int n;
while(cin >> n){
if(!n) break;
for(int i = 1;i <= n;i++){
cin >> a[i];
}
int maxx = INT_MIN;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
for(int k = 1;k <= n;k++){
for(int l = 1;l <= n;l++){
if(i!=j && i!=k && i!=l && j!=k && j!=l && k!=l){
if(a[i] == a[j] + a[k] + a[l])
maxx = max(maxx,a[i]);
}
}
}
}
}
if(maxx != INT_MIN){
cout << maxx << "\n";
}else{
cout << "no solution\n";
}
}
}
# C003 半素数 (opens new window)
# 题目描述
素数的定义:对于一个大于1的正整数,如果除了1和它本身没有其他的正约数了,那么这个数就称为素数。例如,2,11,67,89是素数,8,20,27不是素数。 半素数的定义:对于一个大于1的正整数,如果它可以被分解成2个素数的乘积,则称该数为半素数,例如6是一个半素数,而12不是。 你的任务是判断一个数是否是半素数。
# 输入
输入文件中有多个测试数据,每个测试数据包含一个整数N,2<=N<=1,000,000。
# 输出
对每个测试数据,如果N是半素数,则输出YES,否则输出NO。
# 样例输入 复制
3 4 6 12# 样例输出 复制
NO YES YES NO
# 思路:
这道题就按题意模拟即可~
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
bool isPrime(int n){
if(n <= 1) return false;
if(n == 2) return true;
for(int i = 2;i * i <= n;i++){
if(n % i == 0) return false;
}
return true;
}
int main(){
int n;
while(cin >> n){
int flag = 0;
for(int i = 2;i <= n;i++){
for(int j = 2;j <= n;j++){
if(i * j == n && isPrime(i) && isPrime(j)){
flag = 1;
}
}
}
if(flag) cout << "YES\n";
else cout << "NO\n";
}
}
# C004 棍子的膨胀 (opens new window)
# 题目描述
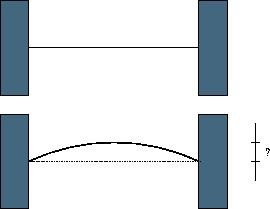
当一根长度为L的细长金属棍子加热n度后,它会膨胀到一个新的长度L’=(1+n*C)*L,其中C为该金属的热膨胀系数。 当一根细长的金属棍子固定在两堵墙之间,然后加热,则棍子会变成圆弓形,棍子的原始位置为该圆弓形的弦,如图所示。
图 膨胀的金属棍子(上为膨胀前,下为膨胀后) 你的任务是计算棍子中心的偏离距离。
# 输入
输入文件包含多个测试数据,每个测试数据占一行。每个测试数据包含3个非负整数:棍子的初始长度,单位为毫米;加热前后的温差,单位为度;该金属的热膨胀系数。输入数据保证膨胀的长度不超过棍子本身长度的一半。输入文件的最后一行为3个负数,代表输入结束,该测试数据不需处理。
# 输出
对每个测试数据,输出金属棍子中心加热后偏离的距离,单位为毫米,保留小数点后3位有效数字。
# 样例输入 复制
1000 100 0.0001 15000 10 0.00006 10 0 0.001 -1 -1 -1# 样例输出 复制
61.329 225.020 0.000
# 思路:
这道题用三角函数去算,也就是考虑到这么一个圆弧(不能认为是三角形,否则误差太大),然后通过数学计算(读者自行画画图)去得出偏移量,然后用二分去算。
注意:这道题的精度需要调高一点~
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
const double PI = acos(-1.0);
const double EPS = 1e-12;
int main() {
double l, n, c, len;
while (cin >> l >> n >> c) {
if (l < 0 || n < 0 || c < 0) break;
if (l <= EPS || n <= EPS || c <= EPS) {
cout << fixed << setprecision(3) << "0.000" << "\n";
continue;
}
len = (1.0 + n * c) * l;
double low = 0;
double high = PI;
double mid;
// 二分去逼近
while (high - low > EPS) {
mid = (high + low) / 2;
double temp = (l * mid) / (sin(mid / 2) * 2);
if (temp >= len) high = mid;
else low = mid;
}
cout << fixed << setprecision(3) << (l / 2) * tan(mid / 4) << "\n";
}
return 0;
}
# C005 电缆主 (opens new window)
# 题目描述
奶牛的居民决定举办一场编程区域赛。裁判委员会自告奋勇并宣称要举办有史以来最公正的比赛。队员们的电脑采用“星型”拓扑结构互连(也就是说要把所有电脑都连在一个中央集线器上)。为了让比赛尽可能公正,裁判委员会的头头们决定:将比赛队员们平均地安置在集线器周围,距离集线器有一个相同的距离。 裁判委员会为了采买网络电缆,联系了一家当地的网络方案提供商,要求他们提供一些登等长的电缆。这些电缆应越长越好,从而使得队员们与其他队员的距离越大。 这家公司的电缆工来办这件事。他知道仓库里每个电缆的长度(精确到厘米)。他每次切割电缆时的精度也是厘米。但他现在不知切多少,所以完全茫然中。 你要写个程序计算出一条电缆最多多长使之可以提供一定能够数目的电缆,帮着这位电缆工完成任务。
# 输入
第一行是两个整数N和K,N(1<=N<=10000)是仓库里的电缆数,K(1<=K<=10000)是所需电缆数。接下来的N行每一行一个数,表示电缆的长度(单位是米)。电缆长度最小为1米,最大为100千米。每个表示长度的数均表示为带两位小数的浮点数(即精确到厘米)。
# 输出
所需的电缆一条最长有多少米(精确到厘米,即保留小数点两位)。如果不能提供K条大于等于1厘米的等长电缆就输出“0.00”。
# 样例输入 复制
4 11 8.02 7.43 4.57 5.39# 样例输出 复制
2.00
# 思路:
最开始读题的时候,其实觉得有点难懂,其实就是问你,如果每一段电缆的长度为xxx,能否裁出k段电缆(从读入的所有电缆中)。
这道题其实看完就可以想到二分了,因为这是个连续的事情:电缆长度越大,电缆数量越少。所以我们要找到一个合适的长度,让电缆数量满足题意,并且尽可能地大。
特判好像不用管【雾】
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
double a[10005];
int n,k;
double eps = 1e-12;
bool check(double mid){
int cnt = 0;
for(int i = 1;i <= n;i++){
cnt += a[i] / mid;
}
return cnt >= k;
}
int main(){
cin >> n >> k;
double maxx = 0;
for(int i = 1;i <= n;i++){
cin >> a[i];
maxx = max(maxx,a[i]);
}
double l = 0;
double r = maxx;
while(r - l > eps){
double mid = (l + r) / 2.0;
if(check(mid)){
l = mid;
}else{
r = mid;
}
}
cout << fixed << setprecision(2) << l << "\n";
}
# C006 宝贝鱼 (opens new window)
# 题目描述
你刚刚从奶牛搬到一个大城市里。这里的人说一种让人理解不能的外文方言。万幸,你有本字典可以帮助你理解。
# 输入
输入包含多达100,000个字典词条,然后是一个空行,然后是一条消息,这条消息包含多达100,000个单词。每个词条占一行,先是一个英语单词,然后是一个空格,然后是一个外文方言词。一个方言词在字典中出现不超过一次。消息是一个外文方言词序列,一个词占一行。每个词是一个最长为10的小写字母序列。
# 输出
将消息的外文词翻译成英语,一个词一行。查不到的词应该翻译成“eh”。
# 样例输入 复制
dog ogday cat atcay pig igpay froot ootfray loops oopslay atcay ittenkay oopslay# 样例输出 复制
cat eh loops
# 思路:
map的简单实现~如果熟悉map的使用,应该不需要什么思考的。
当然,如果不用map的话,这道题的思路应该是,读入所有字典(结构体处理),然后进行结构体排序,最后使用二分去字典结构体数组里查找是否存在该单词。但是这个写法太麻烦了,读者可以自行实现~
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int main(){
map<string,string> mp;
string s;
while(getline(cin,s)){
if(s == "\0") break;
string a = "",b = "";
int flag = 0;
for(int i = 0;i < s.size();i++){
if(s[i] == ' '){
flag = 1;
continue;
}
if(!flag) a += s[i];
else b += s[i];
}
mp[b] = a;
}
while(cin >> s){
if(mp.find(s) != mp.end()){
cout << mp[s] << "\n";
}else{
cout << "eh\n";
}
}
}
# C007 星空 (opens new window)
# 题目描述
将夜空抽象成二维平面,每个星星一个(X,Y)坐标。这些点可以形成多少正方形?
# 输入
多组输入。对于每组数据,第一行是n(1<=n<=1000)表示已知星星数,然后是n行,每行一个坐标值。坐标绝对值小于20000。n=0表示结束。
# 输出
对于每组数据输出形成正方形的个数。
# 样例输入 复制
4 1 0 0 1 1 1 0 0 0# 样例输出 复制
1
# 思路:
这道题就是读入结构体,然后去双循枚举点,然后去假设枚举的两个点是正方形的一条边,去寻找另外两个点是否存在【可以通过现有点推出】。笔者原本的写法是用set排序,然后用set内置的查询去count。但是不知道为何会wa,可能是哪里没考虑到?所以还是换成了二分的写法,即去所有点里二分查找【二分的前提是排序】。
# 代码C++:
#include <bits/stdc++.h>
using namespace std;
struct node {
int x, y;
};
bool cmp(const node &a, const node &b) {
if (a.x == b.x) return a.y < b.y;
return a.x < b.x;
}
bool find(const vector<node> &stars, int x, int y) {
int left = 0, right = stars.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (stars[mid].x == x && stars[mid].y == y) return true;
if (cmp({x, y}, stars[mid])) right = mid - 1;
else left = mid + 1;
}
return false;
}
int main() {
int n;
while (cin >> n) {
if (n == 0) break;
vector<node> stars(n);
for (int i = 0; i < n; ++i) {
cin >> stars[i].x >> stars[i].y;
}
sort(stars.begin(), stars.end(), cmp);
int count = 0;
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
int x1 = stars[i].x;
int y1 = stars[i].y;
int x2 = stars[j].x;
int y2 = stars[j].y;
int x3 = x1 + (y1 - y2);
int y3 = y1 - (x1 - x2);
int x4 = x2 + (y1 - y2);
int y4 = y2 - (x1 - x2);
if (find(stars, x3, y3) && find(stars, x4, y4)) {
count++;
}
}
}
cout << count / 2 << "\n";
}
return 0;
}
# C008 星球穿梭 (opens new window)
# 题目描述
又一届的“穿梭星球“比赛开始了。这项比赛将在星球排到一排的赛道上进行,在赛道上组委会已经选择好了起点(起点在0位置)和终点(在L位置)的星球,在其中间有N个星球,参赛选手只能从当前的星球穿梭到最近的星球。为了提高难度,组委会会移去一部分星球,加大选手的最小穿梭距离。但是由于经费有限,组委会只会移去M个星球。现在需要计算出当前选手的最大最小穿梭距离。
# 输入
第一行包括L,N,M(1 <= L <= 1000,0 <= M <= N <= 1000)分别表示起点和终点的距离,起点与终点之间的星球数以及组委会移去的星球个数。 接下来N行,每行一个整数Di(0 < D < L)表示起点与当前星球的距离。保证距离从小到大给出,且不会有两个星球出现到同一位置,起点和终点的星球是不能被移走。
# 输出
一个整数,表示穿梭距离的最大值。
# 样例输入 复制
25 5 2 2 11 14 17 21# 样例输出 复制
4
# 思路:
笔者一开始读了半天没读懂题意,然后才反应过来求的是“最大“的”最小穿梭距离“,也就是说,我希望让最小间距尽可能大【通过删除星球】。
然后再仔细一读,这题不就是跳石头这道题最经典的二分题目嘛!(必会)
那么就直接看代码吧,也就是二分枚举最小距离,然后判断要达到这个最短距离,需要移除多少个星球,如果要移除的太多就不行。
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int a[10005];
int L,n,m;
int check(int k){
int now = 0;
int cnt = 0;
for(int i = 1;i <= n+1;i++)
{
if (a[i] - a[now] < k)
cnt++;
else
now = i;
}
if (cnt <= m)
return 1;
else
return 0;
}
int main(){
cin >> L >> n >> m;
for (int i = 1; i <= n; i++){
cin >> a[i];
}
a[n+1] = L;
int ans, l = 0, r = L;
while (l <= r){
int mid = (l + r) / 2;
if (check(mid)){
ans = mid;
l = mid + 1;
}
else
r = mid - 1;
}
cout << ans << "\n";
}
# C009 排列硬币 (opens new window)
# 题目描述
你总共有 n枚硬币,并计划将它们按阶梯状排列。对于一个由k行组成的阶梯,其第i行必须正好有i枚硬币。阶梯的最后一行 可能 是不完整的。
给你一个数字n,计算并返回可形成 完整阶梯行 的总行数。
# 输入
输入第一行为测试数据的组数,接下来的每行有一个整数n代表硬币的个数,且1 <= n <= 231 - 1
# 输出
每行输入对应一个输出,为“完整阶梯行”的数量
# 样例输入 复制
2 5 8# 样例输出 复制
2 3
# 思路:
这道题我们就可以模拟一遍,就是从第一层一直加到最后一层。
当然也可以用等差数列的公式来求,然后求到比n还大之后再减1即可【这个写法可以避开一些问题】
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
void solve(){
int n;
cin >> n;
int sum = 0;
int cnt = 0;
int flag = 1;
while(sum <= n){
cnt++;
sum = 0;
sum += (1 + cnt) * cnt / 2;
}
cout << cnt - 1 << "\n";
}
int main(){
int t;
cin >> t;
while(t--){
solve();
}
}