# NENUOJ 之 算法2递归A
# 前言
考虑到进入大二上了,所以代码主要以C++的形式给出,倘若读者擅长使用C语言,影响也不会很大~
# A001 猴子吃桃 (opens new window)
# 题目描述
猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半另加一个。到第10天早上想再吃时,就只剩下一个桃子了。求第1天共摘了多少个桃子。
# 输入
输入第一行为正整数n,为测试数据组数。后面n行为测试数据,每组测试数据包括两个整数m,k,分别表示第m(m>1)天后剩余的桃子数k(k>=0)。
# 输出
输出猴子第一天摘的桃子数,每组数据占一行。
# 样例输入 复制
2 2 2 3 0# 样例输出 复制
6 6
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
while(n--){
int m,k;
cin >> m >> k;
for(int i = m ;i > 1;i--){
k += 1;
k *= 2;
}
cout << k << "\n";
}
}
# A002 最大公约数 (opens new window)
# 题目描述
输入两个正整数,求其最大公约数。 数论中有一个求最大公约数的算法称为辗转相除法,又称欧几里德算法。其基本思想及执行过程为(设m为两正整数中较大者,n为较小者): (1)令u=m,v=n; (2)取u对v的余数,即r=u%v,如果r的值为0,则此时v的值就是m和n的最大公约数,否则执行第(3)步; (3)u=v,v=r,即u的值为v的值,而v的值为余数r。并转向第(2)步。
# 输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括两个正整数m和n。
# 输出
n行,每行输出对应一个输入。输出应是一个正整数,为m和n的最大公约数。
# 样例输入 复制
2 48 32 15 5# 样例输出 复制
16 5
# 代码C++ 代码一:
#include<bits/stdc++.h>
using namespace std;
int ggcd(int a,int b){
return b == 0 ? a : ggcd(b,a % b);
}
int main(){
int n;
cin >> n;
while(n--){
int a,b;
cin >> a >> b;
cout << ggcd(a,b) << "\n";
}
}
# 代码C++ 代码二:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin >> n;
while(n--){
int a,b;
cin >> a >> b;
cout << __gcd(a,b) << "\n";
}
}
# A003 经典的Hanoi(汉诺塔)问题 (opens new window)
# 题目描述
有一个汉诺塔,塔内有A,B,C三个柱子。起初,A柱上有n个盘子,依次由大到小、从下往上堆放,要求将它们全部移到C柱上;在移动过程中可以利用B柱,但每次只能移到一个盘子,且必须使三个柱子上始终保持大盘在下,小盘在上的状态。要求编程输出移动的步骤。
# 输入
输入文件中包含多行,每行为一个整数n,代表初始A柱子上的盘子的个数。
# 输出
对输入文件中的每个整数n列出具体的汉诺塔移动步骤。两组输出之间有一空行。
# 样例输入 复制
3 1# 样例输出 复制
A-->C A-->B C-->B A-->C B-->A B-->C A-->C A-->C
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
void move(char a,char b){
cout << a << "-->" << b << "\n";
}
void hanoi(int n, char a, char b, char c){
if (n == 1)
move(a,c);
else{
hanoi(n - 1,a,c,b);
move(a,c);
hanoi(n - 1,b,a,c);
}
}
int main(){
int n;
while(cin >> n){
hanoi(n,'A','B','C');
cout << "\n";
}
}
# A004 菲波那契数列 (opens new window)
# 题目描述
菲波那契数列是指这样的数列: 数列的第一个和第二个数都为1,接下来每个数都等于前面2个数之和。给出一个正整数a,要求菲波那契数列中第a个数是多少。
# 输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a(1 <= a <= 20)。
# 输出
输出有n行,每行输出对应一个输入。输出应是一个正整数,为菲波那契数列中第a个数的大小。
# 样例输入 复制
4 5 2 19 1# 样例输出 复制
5 1 4181 1
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int f[1000];
void cal(){
f[0] = 0;
f[1] = 1;
for(int i = 2;i <= 20;i++){
f[i] = f[i - 1] + f[i - 2];
}
}
int main(){
int n;
cin >> n;
cal();
while(n--){
int a;
cin >> a;
cout << f[a] << "\n";
}
}
# A005 另一个Fibonacci数列 (opens new window)
# 题目描述
定义另外一个Fibonacci数列:F(0)=7,F(1)=11,F(n)=F(n-1)+F(n-2),(n≥2)。
# 输入
输入文件中包含多行,每行为一个整数n,n<1000000。
# 输出
对输入文件中的每个整数n,如果F(n)能被3整除,输出yes,否则输出no。
# 样例输入 复制
0 1 2 3# 样例输出 复制
no no yes no
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
while(cin >> n){
if(n % 4 == 2) cout << "yes\n";
else cout << "no\n";
}
}
# A006 分形(Fractal) (opens new window)
# 题目描述
分形是存在“自相似”的一个物体或一种量,从某种技术角度来说,这种“自相似”是全方位的。 盒形分形定义如下: 度数为1的分形很简单,为: X
度数为2的分形为:
X X
X
X X
如果用B(n-1)代表度数为n-1的盒形分形,则度数为n的盒形分形可以递归地定义为:
B(n-1) B(n-1)
B(n-1)
B(n-1) B(n-1)
你的任务是输出度数为n的盒形分形。
# 输入
输入文件包含多个测试数据,每个测试数据占一行,包含一个正整数n,n ≤ 7。输入文件的最后一行为-1,代表输入结束。
# 输出
对每个测试数据,用符号“X”表示输出盒形分形。在每个测试数据对应的输出之后输出一个短划线符号“-”,在每行的末尾不要输出任何多余的空格,否则得到的是“格式错误”的结果。
# 样例输入 复制
2 3 -1# 样例输出 复制
X X X X X - X X X X X X X X X X X X X X X X X X X X X X X X X
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e3;
char a[MAXN][MAXN];
void solve(int x,int y,int n){
int l = (int)pow(3,n - 2);
if(n == 1){
a[x][y] = 'X';
return;
}
if(n){
solve(x,y,n - 1);
solve(x + l,y + l,n - 1);
solve(x + 2*l,y,n - 1);
solve(x,y + 2*l,n - 1);
solve(x + 2*l,y + 2*l,n - 1);
}
}
int main(){
int n;
int cnt = 0;
while(cin >> n){
if(n == -1) break;
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
a[i][j] = ' ';
}
}
if(cnt != 0)cout << "-" << "\n";
cnt++;
solve(0,0,n);
int m = (int)pow(3,n - 1);
for(int i = 0;i < m;i++){
int maxx = 0;
for(int j = 0;j < m;j++){
if(a[i][j] == 'X'){
maxx = j;
}
else a[i][j] = ' ';
}
a[i][maxx + 1] = '\0';
}
for(int i = 0;i < m;i ++){
cout << a[i] << "\n";
}
}
}
# A007 二叉树 (opens new window)
# 题目描述
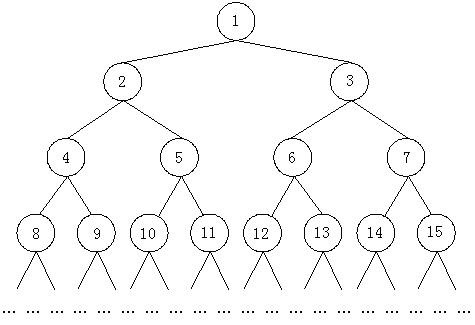
如图所示,由正整数1, 2, 3, ...组成了一棵无限大的二叉树。从某一个结点到根结点(编号是1的结点)都有一条唯一的路径,比如从10到根结点的路径是(10, 5, 2, 1),从4到根结点的路径是(4, 2, 1),从根结点1到根结点的路径上只包含一个结点1,因此路径就是(1)。对于两个结点x和y,假设他们到根结点的路径分别是$(x_1, x_2, ... ,1)$和$(y_1, y_2, ... ,1)$(这里显然有$x = x_1,y = y_1$),那么必然存在两个正整数i和j,使得从xi 和 yj开始,有$x_i = y_j , x_i + 1 = y_j + 1, x_i + 2 = y_j + 2,... $现在的问题就是,给定x和y,要求$x_i$(也就是$y_j$)。
# 输入
输入有多行,每行包括两个正整数x和y,这两个正整数都不大于1000。
# 输出
每行输出只有一个正整数$x_i$。
# 样例输入 复制
10 4# 样例输出 复制
2
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int f[1000];
int com(int x,int y){
if(x == y) return x;
if(x > y) return com(x / 2,y);
return com(x,y / 2);
}
int main(){
int x,y;
while(cin >> x >> y)
cout << com(x,y) << "\n";
return 0;
}
# A008 波兰表达式 (opens new window)
# 题目描述
波兰表达式是一种把运算符前置的算术表达式,例如普通的表达式2 + 3的波兰表示法为+ 2 3。波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的波兰表示法为* + 2 3 4。本题求解波兰表达式的值,其中运算符包括+ - * /四个。
# 输入
输入第一行为一个整数n,然后是n行,每行为一组测试数据,其中运算符和运算数之间都用空格分隔,运算数是浮点数。
# 输出
输出n行,每行表达式的值,保留3位小数输出。
# 样例输入 复制
1 * + 11.0 12.0 + 24.0 35.0# 样例输出 复制
1357.000
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
double solve()
{
char s[10000];
cin >> s;
switch(s[0])
{
case '+': return solve() + solve();
case '-': return solve() - solve();
case '*': return solve() * solve();
case '/': return solve() / solve();
default : return atof(s);
}
}
int main(){
int n;
cin >> n;
while(n--){
printf("%.3lf\n",solve());
}
return 0;
}
# A009 放苹果 (opens new window)
# 题目描述
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法(用K表示)?注意:5,1,1和1,5,1 是同一种分法。
# 输入
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1 <= M,N <= 10。
# 输出
对输入的每组数据M和N,用一行输出相应的K。
# 样例输入 复制
1 7 3# 样例输出 复制
8
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int dfs(int m,int n){
if(m==0 || n==1) {
return 1;
}
if(n > m){
return dfs(m,m);
}
else{
return dfs(m,n - 1) + dfs(m - n,n);
}
}
void solve(){
int m,n;
cin >> m >> n;
cout << dfs(m,n) << "\n";
}
int main(){
int t = 1;
cin >> t;
while(t--) solve();
}
# A010 递归练习1 (opens new window)
# 题目描述
有5个人坐在一起,问第5个人多少岁?他说比第4个人大两岁。问第4个人的岁数,他说比第3个人大两岁。问第3个人的岁数,又说比第2个人大两岁。问第2个人的岁数,说比第1个人大两岁。最后问第1个人的岁数,他说是10岁。请问第5个人多少岁?
# 输入
输入有多行,每行3个整数,依次为m,n,k。m表示一共有几个人,n表示大的岁数,k表示第一个人的岁数。
# 输出
输出第m个人的岁数,每个一行。
# 样例输入 复制
5 2 10# 样例输出 复制
18
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int main(){
int m,n,k;
while(cin >> m >> n >> k){
cout << k + (m - 1) * n << "\n";
}
}
# A011 递归练习2 (opens new window)
# 题目描述
根据递推式子C(m,n)=C(m-1,n)+C(m-1,n-1),求组合数C(m,n)。注意递推的终止条件是C(m,1)=m;以及一些m和n取值的一些特殊情况,如m < 0或n < 0或m < n时,C(m,n)值为0,m和n相等时,C(m,n)=1等。
# 输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数m和一个正整数n。
# 输出
输出组合数C(m,n)。
# 样例输入 复制
2 1 100 100 1# 样例输出 复制
0 100
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int C(int m,int n){
if(n == 1) return m;
if(m < 0 || n < 0 || m < n){
return 0;
}
if(m == n) return 1;
return C(m - 1,n) + C(m - 1,n - 1);
}
int main(){
int t;
cin >> t;
while(t--){
int m,n;
cin >> m >> n;
cout << C(m,n) << "\n";
}
}
# A012 递归练习3 (opens new window)
# 题目描述
核反应堆中有α和β两种粒子。每秒钟内一个α粒子可以产生3个β粒子,而一个β粒子可以产生1个α粒子和2个β粒子。若在t=0时刻反应堆中有一个α粒子,求t时刻反应堆中分别有多少个α粒子和β粒子。
# 输入
输入有多个整数t,每个一行。
# 输出
输出t时刻反应堆里分别有多少个α粒子和β粒子。
# 样例输入 复制
6# 样例输出 复制
183 546
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int main(){
int t;
int a[100],b[100];
while(cin >> t){
a[0] = 1;
b[0] = 0;
for(int i = 1;i <= t;i++){
a[i] = b[i - 1];
b[i] = 3 * a[i - 1] + 2 * b[i - 1];
}
cout << a[t] << " " << b[t] << "\n";
}
}
# A013 红与黑 (opens new window)
# 题目描述
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
# 输入
包括多个数据集合。每个数据集合的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中,每行包括W个字符。每个字符表示一块瓷砖的颜色,规则如下 1)‘.’:黑色的瓷砖; 2)‘#’:白色的瓷砖; 3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。 当在一行中读入的是两个零时,表示输入结束。
# 输出
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
# 样例输入 复制
6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 0 0# 样例输出 复制
45
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
char mx[100][100];
int vis[100][100];
int w,h;
int x,y;
int dfs(int x,int y){
if(mx[x][y] == '#') return 0;
if(x <= 0 || y <= 0 || x > h || y > w) return 0;
if(vis[x][y]) return 0;
vis[x][y] = 1;
return 1 + dfs(x - 1,y) + dfs(x + 1,y) + dfs(x,y - 1) + dfs(x,y + 1);
}
int main(){
while(cin >> w >> h){
if(!w || !h) break;
for(int i = 1;i <= h;i++){
for(int j = 1;j <= w;j++){
cin >> mx[i][j];
vis[i][j] = 0;
if(mx[i][j] == '@') x = i,y = j;
}
}
cout << dfs(x,y) << "\n";
}
}
# A014 城堡问题 (opens new window)
# 题目描述
1 2 3 4 5 6 7 #############################
1 # | # | # | | #
#####---#####---#---#####---#
2 # # | # # # # #
#---#####---#####---#####---#
3 # | | # # # # #
#---#########---#####---#---#
4 # # | | | | # #
#############################
(图 1)
‘#’ = Wall ‘|’ = No wall '-' = No wall
图1是一个城堡的地形图。请你编写一个程序,计算城堡一共有多少房间,最大的房间有多大。城堡被分割成m*n(m≤50,n≤50)个方块,每个方块可以有0~4面墙。
# 输入
程序从标准输入设备读入数据。第一行是两个整数,分别是南北向、东西向的方块数。在接下来的输入行里,每个方块用一个数字(0≤p≤50)描述。用一个数字表示方块周围的墙,1表示西墙,2表示北墙,4表示东墙,8表示南墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两次,方块(1,1)的南墙同时也是方块(2,1)的北墙。输入的数据保证城堡至少有两个房间。
# 输出
城堡的房间数、城堡中最大房间所包括的方块数。
# 样例输入 复制
4 7 11 6 11 6 3 10 6 7 9 6 13 5 15 5 1 10 12 7 13 7 5 13 11 10 8 10 12 13# 样例输出 复制
5 9
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
const int dir[4][2] = { {0, -1}, {-1, 0}, {0, 1}, {1, 0} };
const int mask[4] = {1, 2, 4, 8};
int rows, cols;
vector<vector<int>> mx, vis;
int ans = 0, maxx = 0, cnt = 0;
void dfs(int x, int y, int step) {
if (vis[x][y]) return;
cnt++;
vis[x][y] = step;
for (int d = 0; d < 4; ++d) {
int nx = x + dir[d][0];
int ny = y + dir[d][1];
if (nx >= 1 && nx <= rows && ny >= 1 && ny <= cols && !vis[nx][ny]) {
if ((mx[x][y] & mask[d]) == 0) {
dfs(nx, ny, step);
}
}
}
}
int main() {
cin >> rows >> cols;
mx.resize(rows + 1, vector<int>(cols + 1));
vis.resize(rows + 1, vector<int>(cols + 1, 0));
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
cin >> mx[i][j];
}
}
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
if (!vis[i][j]) {
ans++;
cnt = 0;
dfs(i, j, ans);
maxx = max(cnt, maxx);
}
}
}
cout << ans << "\n";
cout << maxx << "\n";
return 0;
}
# A015 分解因式 (opens new window)
# 题目描述
给出一个正整数a,要求分解成若干个正整数的乘积,即a = a1 * a2 * a3 * ... * an,并且1 < a1 <= a2 <= a3 <= ... <= an,问这样的分解的种数有多少。注意到a = a也是一种分解。
# 输入
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a (1 < a < 32768)。
# 输出
n行,每行输出对应一个输入。输出应是一个正整数,指明满足要求的分解的种数。
# 样例输入 复制
2 2 20# 样例输出 复制
1 4
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int cnt = 1;
void dfs(int m,int a){
for(int i = m;i * i <= a;i++){
if(a % i == 0){
cnt++;
dfs(i,a / i);
}
}
}
int main(){
int n;
cin >> n;
while(n--){
cnt = 1;
int a;
cin >> a;
dfs(2,a);
cout << cnt << "\n";
}
}
# A016 数字拼凑 (opens new window)
# 题目描述
现在给你这样一个任务,要求找出具有下列性质数的个数(包含输入的正整数 n)。 先输入一个正整数 n(n <= 500),然后对此正整数按照如下方法进行处理:
- 不作任何处理;
- 在它的左边拼接一个正整数,但该正整数不能超过原数的一半或者是上一个被拼接数的一半;
- 加上数后,继续按此规则进行处理,直到不能再加正整数为止。
# 输入
一个正整数n。
# 输出
一个正整数,表示具有该性质数的个数。
# 样例输入 复制
6# 样例输出 复制
6
# 代码C++:
#include<bits/stdc++.h>
using namespace std;
int cnt;
void dfs(int m){
cnt++;
for (int i = 1;i <= m/2;i++)
dfs(i);
}
int main(){
int n;
cin >> n;
dfs(n);
cout << cnt << "\n";
return 0;
}