# NENUOJ 之 算法1第3章
# 3001 最大公约数 (opens new window)
# 题目描述
输入两个整数a,b (1 <= a,b <= 100000000),请编写程序求出他们的最大公约数。
# 输入
第一个正整数n表示测试数据的个数,接下来的n行每行有两个整数a和b,空格隔开。
# 输出
输出n行,每行输出对应a,b的最大公约数。
# 样例输入 复制
3 12 8 25 10 21 63# 样例输出 复制
4 5 21
# 思路:
最大公约数用辗转相除法写就好,辗转相除法的写法自行查询~
# 代码C语言:
#include<stdio.h>
int gcd(int x,int y){
return x % y ? gcd(y,x % y) : y;
}
int main(){
int a,b;
int n;
scanf("%d",&n);
while(n--){
scanf("%d %d",&a,&b);
printf("%d\n",gcd(a,b));
}
return 0;
}
# 3002 假票统计 (opens new window)
# 题目描述
由于你们团队在国际大学生诗歌大赛上取得的巨大成就,你们学校决定为你们召开一次庆功鸡尾酒会,到来的人数大大超出了预期。 然而庆功会的主管却抱怨发现了有人使用假票,实际的门票是从1到N (N <= 10000),主管怀疑有人采用复印、打印等手段伪造了门票。他把所有收上来的门票拿给你,要求你编写程序,统计所有门票中存在假票的门票数。
# 输入
输入文件中包含多组测试数据,每组测试数据占两行。第1行包括两个整数N和M,分别表示门票的初始总张数和参加晚会的总人数 (1 <= N <= 10000,1 <= M <= 20000)。第2行为M个整数Ti ,表示收到的M张门票的号码(1 <= Ti <= N)。输入文件最后一行为0 0,表示输入结束。
# 输出
对每组输入测试数据,输出一个整数,占一行,表示收上来的门票中共有多少种票被伪造过。
# 样例输入 复制
5 5 3 3 1 2 4 6 10 6 1 3 6 6 4 2 3 1 2 0 0# 样例输出 复制
1 4
# 思路:
注意读题!这道题要求的是有几种票被伪造过,我们可以用一个数组记录每一种票被收上了几张,如果一种票被收上来了好多张,说明这一种票被伪造了。
注意,有多组测试数据,所以每一组数据结束之后,要注意清空数组和变量。记得换行~
局部变量的数组不能开太大,1e4(即10000的数量级)的数据量就很大了,如果再大,就应当开全局变量哦!
# 代码C语言:
#include<stdio.h>
int main(){
int n,m;
while(~scanf("%d %d",&n,&m)){
int vis[20005] = {0};
if(n == 0 && m == 0) break;
for(int i = 1;i <= m;i++){
int ticket;
scanf("%d",&ticket);
vis[ticket]++;
}
int cnt = 0;
for(int i = 0;i < 20005;i++){
if(vis[i] > 1) cnt++;
}
printf("%d\n",cnt);
}
}
# 3003 折半处理 (opens new window)
# 题目描述
对于一个数n,如果是偶数,就把n砍掉一半;如果是奇数,把n变成 3 * n + 1后砍掉一半,直到该数变为1为止。 请计算需要经过几步才能将n变到1,具体可见样例。
# 输入
包含多个测试数据,每个测试数据包含一个整数n,当n为0 时表示输入结束。(1 <= n <= 10000)。
# 输出
对于每组测试数据请输出一个数,表示需要经过的步数,每组输出占一行。
# 样例输入 复制
3 1 0# 样例输出 复制
5 0
# 思路:
这道题就是简单的模拟,但是可以学习一下笔者的代码二的代码写法,有些写法还是很值得学习的。
用 if(!n) 代替 if(n == 0) ,用 if(n & 1) 代替 if(n % 2 == 1) 。
# 代码C语言 写法一:
#include<stdio.h>
int main(){
int n;
while(~scanf("%d",&n)){
if(n == 0) break;//也可以写成 if(!n) break; 这是同一个含义哦!
int cnt = 0;
while(n != 1){
if(n % 2 == 0){
n /= 2;
}else{
n = n*3 + 1;
n /= 2;
}
cnt++;
}
printf("%d\n",cnt);
}
}
# 代码C语言 写法二:
#include<stdio.h>
int main(){
int n;
while(~scanf("%d",&n)){
if(!n) break;
int cnt = 0;
while(n != 1){
if(n & 1){
n = n*3 + 1;
n /= 2;
}else{
n /= 2;
}
cnt++;
}
printf("%d\n",cnt);
}
}
# 3004 棋盘上的距离 (opens new window)
# 题目描述
国际象棋的棋盘是黑白相间的8 * 8的方格,棋子放在格子中间。如下图所示:
国际象棋棋盘示意图
王、后、车、象的走子规则如下: (1)王:横、直、斜都可以走,但每步限走一格。 (2)后:横、直、斜都可以走,每步格数不受限制。 (3)车:横、竖均可以走,不能斜走,格数不限。 (4)象:只能斜走,格数不限。 写一个程序,给定起始位置和目标位置,计算王、后、车、象从起始位置走到目标位置所需的最少步数。
# 输入
第一行是测试数据的组数t(0 <= t <= 20)。以下每行是一组测试数据,每组包括棋盘上的两个位置,第一个是起始位置,第二个是目标位置。位置用字母-数字的形式表示,字母从“a”到“h”,数字从“1”到“8”。
# 输出
对输入的每组测试数据,输出王、后、车、象所需的最少步数。如果无法到达,就输出“Inf”。
# 样例输入 复制
2 a1 c3 f5 f8# 样例输出 复制
2 1 2 1 3 1 1 Inf
# 思路:
这道题在大一下的时候,困住笔者好长一段时间,是个比较复杂的模拟,下方的写法一就是笔者当时的代码,写法二为笔者写题解时重写的代码。思路很简单,就是去想象(不单纯是模拟),比如像王,斜着走或者直着走,肯定能走到,并且步数就是距离之差的最大值。像后,一定能走到,就三种情况,0、1、2,0就是在原地,1就是在同个横轴或者竖轴或者斜轴上,2就是前两种情况之外。车也一定,0就是在原地,1就是在同个横轴或者竖轴上,2就是前两种情况之外。
最复杂的就是象的情况,白象不走黑格,黑象不走白格,首先,如果起点和终点一样,就是0(即在原地),如果起点和终点是斜轴的关系,那步数就是1,如果横轴+竖轴的距离之和为奇数,说明一定一个在白格,一个在黑格,就是Inf,否则都是步数为2的情况,然后按这个思路写代码就好~读入的方式看自己喜好,可以参考笔者的写法。
# 代码C语言 写法一:
#include<stdio.h>
int main(){
int t;
char str1[1000],str2[1000];
int a1,a2;
scanf("%d",&t);
while(t--){
scanf("%s %s",str1,str2);
int w = str1[1]-str2[1];
int h = str1[0]-str2[0];
if(w<0) w=-w;
if(h<0) h=-h;
if(w==0&&h==0){
printf("0 0 0 0\n");
continue;
}
else{
//king
printf("%d ",w>h?w:h);
//queen
if(w==h||w==0||h==0){
printf("1 ");
}else{
printf("2 ");
}
//car
if(w==0||h==0){
printf("1 ");
}else{
printf("2 ");
}
int temp = w>h?w-h:h-w;
//xiang
if(temp%2!=0){
printf("Inf\n");
}
else if(w==h){
printf("1\n");
}else{
printf("2\n");
}
}
}
return 0;
}
# 代码C语言 写法二:
#include<stdio.h>
int max(int a,int b){
return a > b ? a : b;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
int cnt1 = 0;
int cnt2 = 0;
int cnt3 = 0;
int cnt4 = 0;
char begin[2];
char end[2];
scanf("%s %s",begin,end);
//王
cnt1 = max(abs(end[0] - begin[0]),abs(end[1] - begin[1]));
//后
if(end[0] == begin[0] && end[1] == begin[1]){
cnt2 = 0;
}
else if(end[0] == begin[0] || end[1] == begin[1] || abs(end[0] - begin[0]) == abs(end[1] - begin[1])){
cnt2 = 1;
}else cnt2 = 2;
//车
if(end[0] == begin[0] && end[1] == begin[1]){
cnt3 = 0;
}else if(end[0] == begin[0] || end[1] == begin[1]){
cnt3 = 1;
}else{
cnt3 = 2;
}
//象
if(end[0] == begin[0] && end[1] == begin[1]){
cnt4 = 0;
}else if(abs(end[0] - begin[0]) == abs(end[1] - begin[1])){
cnt4 = 1;
}else if((abs(end[0] - begin[0]) + abs(end[1] - begin[1])) % 2 == 1){
cnt4 = -1;
}else{
cnt4 = 2;
}
if(~cnt4)//等价于 if(cnt4 != -1) 的写法
printf("%d %d %d %d\n",cnt1,cnt2,cnt3,cnt4);
else printf("%d %d %d Inf\n",cnt1,cnt2,cnt3);
}
return 0;
}
# 3005 小明的A+B (opens new window)
# 题目描述
小明今年3岁了,现在他已经能够认识100以内的非负整数,并且能够进行100以内的非负整数的加法计算; 对于大于等于100的整数,小明仅保留该数的最后两位进行计算,如果计算结果大于等于100,那么小明也仅保留计算结果的最后两位。 例如, 对于小明来说: (1)1234和34是相等的 (2)35+80=15 给定非负整数A和B,你的任务是代表小明计算出A+B的值。
# 输入
输入数据的第一行为一个正整数T,表示测试数据的组数。然后是T组测试数据,每组测试数据包含两个非负整数A和B(A和B均在int型可表示的范围内)。
# 输出
对于每组测试数据,输出小明A+B的结果。
# 样例输入 复制
2 35 80 15 1152# 样例输出 复制
15 67
# 思路:
思路很容易,就是个很简单的模拟,前面取余,输出也取余就好。
# 代码C语言:
#include<stdio.h>
int main(){
int t;
scanf("%d",&t);
while(t--){
int a,b;
scanf("%d %d",&a,&b);
if(a > 100) a %= 100;
if(b > 100) b %= 100;
printf("%d\n",(a + b) % 100);
}
}
# 3006 奖学金计算 (opens new window)
# 题目描述
某校的惯例是在每学期的期末考试之后发放奖学金。发放的奖学金共有五种,获取的条件各自不同:
- 院士奖学金,每人8000元,期末平均成绩高于80分(>80),并且在本学期内发表1篇或1篇以上论文的学生均可获得;
- 五四奖学金,每人4000元,期末平均成绩高于85分(>85),并且班级评议成绩高于80分(>80)的学生均可获得;
- 成绩优秀奖,每人2000元,期末平均成绩高于90分(>90)的学生均可获得;
- 西部奖学金,每人1000元,期末平均成绩高于85分(>85)的西部省份学生均可获得;
- 班级贡献奖,每人850元,班级评议成绩高于80分(>80)的学生干部均可获得; 只要符合条件就可以得奖,每项奖学金的获奖人数没有限制,每名学生也可以同时获得多项奖学金。例如姚林的期末平均成绩是87分,班级评议成绩82分,同时他还是一位学生干部,那么他可以同时获得五四奖学金和班级贡献奖,奖金总数是4850元。 现在给出若干学生的相关数据,请计算哪些同学获得的奖金总数最高(假设总有同学能满足获得奖学金的条件)。
# 输入
输入的第一行是一个整数N(1 <= N <= 100),表示学生的总数。接下来的N行每行是一位学生的数据,从左向右依次是姓名,期末平均成绩,班级评议成绩,是否是学生干部,是否是西部省份学生,以及发表的论文数。姓名是由大小写英文字母组成的长度不超过20的字符串(不含空格);期末平均成绩和班级评议成绩都是0到100之间的整数(包括0和100);是否是学生干部和是否是西部省份学生分别用一个字符表示,Y表示是,N表示不是;发表的论文数是0到10的整数(包括0和10)。每两个相邻数据项之间用一个空格分隔。
# 输出
输出包括三行,第一行是获得最多奖金的学生的姓名,第二行是这名学生获得的奖金总数。如果有两位或两位以上的学生获得的奖金最多,输出他们之中在输入文件中出现最早的学生的姓名。第三行是这N个学生获得的奖学金的总数。
# 样例输入 复制
4 YaoLin 87 82 Y N 0 ChenRuiyi 88 78 N Y 1 LiXin 92 88 N N 0 ZhangQin 83 87 Y N 1# 样例输出 复制
ChenRuiyi 9000 28700
# 思路:
这道题就是很简单的模拟,跟着写一遍!
笔者揣测很多同学第一次写这道题目的时候可能会开一个结构体数组去存储,但是根本不需要存储数据,我们只是要最大值和总和而已,所以希望读者可以参考下方的代码写一版更好的!
# 代码C语言:
#include<stdio.h>
#include<string.h>
int max(int a,int b){
return a > b ? a : b;
}
int main(){
int n;
scanf("%d",&n);
int ans = 0;
char res[25];
int total = 0;
for(int i = 1;i <= n;i++){
char name[25];
int aver;
int score;
char flag1;
char flag2;
int paper;
scanf("%s %d %d %c %c %d",name,&aver,&score,&flag1,&flag2,&paper);
int sum = 0;
//期末平均成绩高于80分(>80)
//并且在本学期内发表1篇或1篇以上论文的学生均可获得
if(aver > 80 && paper >= 1) sum += 8000;
//期末平均成绩高于85分(>85)
//并且班级评议成绩高于80分(>80)的学生均可获得
if(aver > 85 && score > 80) sum += 4000;
//期末平均成绩高于90分(>90)的学生均可获得
if(aver > 90) sum += 2000;
//期末平均成绩高于85分(>85)的西部省份学生均可获得
if(aver > 85 && flag2 == 'Y') sum += 1000;
//班级评议成绩高于80分(>80)的学生干部均可获得
if(score > 80 && flag1 == 'Y') sum += 850;
if(sum > ans){
strcpy(res,name);
}
ans = max(ans,sum);
total += sum;
}
printf("%s\n%d\n%d",res,ans,total);
}
# 3007 装箱问题 (opens new window)
# 题目描述
一个工厂生产的产品形状都是长方体,高度都是h,主要有1 * 1,2 * 2,3 * 3,4 * 4,5 * 5,6 * 6等6种。这些产品在邮寄时被包装在一个6 * 6 * h的长方体包裹中。由于邮费很贵,工厂希望减小每个订单的包裹数量以增加他们的利润。因此他们需要一个好的程序帮他们解决这个问题。你的任务就是设计这个程序。
# 输入
输入包括多组测试数据,每一行代表一个订单。每个订单里的一行包括六个整数,用空格隔开,从小到大分别为这6种产品的数量。6个0表示文件结束。
# 输出
针对每个订单输出一个整数,占一行,代表对应的订单所需的最小包裹数。没有多余的空行。
# 样例输入 复制
0 0 4 0 0 1 7 5 1 0 0 0 0 0 0 0 0 0# 样例输出 复制
2 1
# 思路:
这道题比较复杂,我们得画画图来想一下。
这里有个6 * 6的表格。
假设我们有5个6 * 6的产品,就需要5个箱子,所以我们就 cnt 加上6 * 6产品的数量就好。( cnt 表示我们需要的箱子数量)
假设我们有5 * 5的产品,就是下图:
一个5 * 5产品需要一个箱子,并且还可以放下11个1 * 1的箱子。
假设我们有4 * 4的产品,就是下图:
一个4 * 4的产品也需要一个箱子,并且还可以放下5个2 * 2的箱子或者更多的1 * 1的箱子。
假设我们有3 * 3的产品:
可以放下4个3 * 3的箱子,或者其它的组合
依次类推……
所以我们可以按照这个思路去模拟,每次先考虑大产品再考虑放小产品。
但是这道题真的很难实现,如果有耐心的话可以慢慢模拟实现,但是真的真的很容易写错,
笔者一直写错。所以可以参考下面比较抽象的代码,大概思路也差不多,先把6 * 6、5 * 5、4 * 4需要的箱子算上,再加上3 * 3需要的箱子数(c / 4向上取整)。然后考虑这些箱子产生的空位是否足够2 * 2的产品所需,如果不够就再加。然后最后再同样考虑,所有剩下的空格是否足够1 * 1所需,如果不够就再加。
代码大概如下,谨慎参考。
# 代码C语言:
#include<stdio.h>
int k[4]={0,5,3,1};//表示当剩余的3x3产品的数量为0到3个时,可以额外放入2x2产品的数量
//假设多出0个3 * 3,就可以放入0个2 * 2;假设多出1个3 * 3,可以放下5个2 * 2;假设多出2个3 * 3,就可以放下2个2 * 2;假设多出3个3 * 3,就可以放下1个2 * 2
int main(){
int a,b,c,d,e,f;
while(~scanf("%d %d %d %d %d %d",&a,&b,&c,&d,&e,&f)){
if(!a && !b && !c && !d && !e && !f) break;
int ans = 0;
ans += f + e + d + c/4;
if(c % 4 != 0) ans++;
if(b > 5 * d + k[c % 4]){//考虑4 * 4中可以多放入的2 * 2还有3 * 3中还可以多放入的2 * 2
ans += (b - (5 * d + k[c % 4]) + 8) / 9;//这里+8是为了向上取整,没有别的含义,主要就是看看还需要单独为2 * 2开多少个箱子
}
if(a > ans * 36 - (f * 36 - e * 25 - d * 16 - c * 9 - b * 4)){//如果a的数量>剩余1 * 1的个数
ans += (a - (ans * 36 - (f * 36 - e * 25 - d * 16 - c * 9 - b * 4)) + 35) / 36;
//这里+35是为了向上取整,没有别的含义,主要就是看看还需要单独为1 * 1开多少个箱子
}
printf("%d\n",ans);
}
}
# 3008 前m大的数 (opens new window)
# 题目描述
小周想确认一下她的答案是否正确,但是整个的答案是很庞大的表,小周只想让你把答案中最大的M个数告诉她就可以了。 给定一个包含N(N <= 3000)个正整数的序列,每个数不超过5000,对它们两两相加得到的N*(N-1)/2个和,求出其中前M大的数(M <= 1000)并按从大到小的顺序排列。
# 输入
输入可能包含多组数据,其中每组数据包括两行: 第一行两个数N和M, 第二行N个数,表示该序列。
# 输出
对于输入的每组数据,输出M个数,表示结果。输出应当按照从大到小的顺序排列。
# 样例输入 复制
4 4 1 2 3 4 4 5 5 3 6 4# 样例输出 复制
7 6 5 5 11 10 9 9 8
# 思路:
这道题思路也很简单,就是把所有情况枚举一次就好。笔者一开始还排了个序,后来觉得完全不需要,直接暴力枚举所有“两数之和”的情况,然后存储起来,之后从大到小输出就好。
# 代码C语言:
#include<stdio.h>
int a[10000];
int vis[10000];
int main(){
int n,m;
while(~scanf("%d %d",&n,&m)){
for(int i = 0;i < 10000;i++){
vis[i] = 0;
a[i] = 0;
}
for(int i = 1;i <= n;i++){
scanf("%d",&a[i]);
}
for(int i = 1;i <= n;i++){
for(int j = i + 1;j <= n;j++){
int temp = a[i] + a[j];
vis[temp]++;
}
}
for(int i = 10000;i >= 0 && m;i--){
while(vis[i] > 0) {
printf("%d ",i);
vis[i]--;
m--;
}
}
printf("\n");
}
}
# 3009 垂直直方图 (opens new window)
# 题目描述
输入4行全部由大写字母组成的文本,输出一个垂直直方图,给出每个字符出现的次数。注意:只用输出字符的出现次数,不用输出空白字符,数字或者标点符号的输出次数。
# 输入
输入包括4行由大写字母组成的文本,每行上字符的数目不超过80个。
# 输出
输出包括若干行。其中最后一行给出26个大写英文字母,这些字母之间用空格隔开。前面的几行包括空格和星号,每个字母出现几次,就在这个字母的上方输出一个星号。注意:输出的第一行不能是空行。
# 样例输入 复制
THE QUICK BROWN FOX JUMPED OVER THE LAZY DOG. THIS IS AN EXAMPLE TO TEST FOR YOUR HISTOGRAM PROGRAM. HELLO!# 样例输出 复制
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
# 思路:
这道题题意不难理解,就是考虑怎么实现。其实和以前的那些输出空格和星号的题目差不多,就是得观察一下图像。我们的思路就是要计数,看看有多少个ABCD……什么的,然后用*的形式输出出来。我们会发现最高的那个星号就是这个字母出现的次数,我们把这个最大值称为maxx,然后去看看行和列与这个maxx之间的关系,看看什么时候要输出星号,而什么时候输出空格。比如我们用vis数组记录每个字母出现次数,假设A出现5次吧(vis[ 0 ] = 5 ),而maxx是10,那对A来说就是先输出(10 - 5)次空格,再输出5次星号,所以我们就是用 maxx - vis[ j ] 与 i 之间的关系,来考虑最后会怎么样地输出。具体请看代码~
# 代码C语言:
#include<stdio.h>
#include<string.h>
int vis[1000];
int max(int a,int b){
return a > b ? a : b;
}
int main(){
char line[1000];
for(int i = 1;i <= 4;i++){
fgets(line,sizeof(line),stdin);
int len = strlen(line);
for(int i = 0;i < len;i++){
vis[line[i] - 'A']++;
}
}
int maxx = 0;
for(int i = 0;i < 26;i++){
maxx = max(maxx,vis[i]);
}
for(int i = 0;i < maxx;i++){
for(int j = 0;j < 26;j++){
if(maxx - vis[j] > i) printf(" ");
else printf("* ");
}
printf("\n");
}
for(int i = 0;i < 26;i++){
printf("%c ",'A' + i);
}
}
# 3010 肿瘤检测 (opens new window)
# 题目描述
一张CT扫描的灰度图像可以用一个N * N(0 < N < 100)的矩阵描述,矩阵上的每个点对应一个灰度值(整数),其取值范围是0~255。我们假设给定的图像中有且只有一个肿瘤。在图上监测肿瘤的方法如下:如果某个点对应的灰度值小于等于50,则这个点在肿瘤上,否则不在肿瘤上。我们把在肿瘤上的点的数目加起来,就得到了肿瘤在图上的面积。任何在肿瘤上的点,如果它是图像的边界或者它的上下左右四个相邻点中至少有一个是非肿瘤上的点,则该点称为肿瘤的边界点。肿瘤的边界点的个数称为肿瘤的周长。现在给定一个图像,要求计算其中的肿瘤的面积和周长。
# 输入
输入第一行包含一个正整数N(0 < N < 100),表示图像的大小;接下来N行,每行包含图像的一行。图像的一行用N个整数表示(所有整数大于等于0,小于等于255),两个整数之间用一个空格隔开。
# 输出
输出只有一行,该行包含两个正整数,分别为给定图像中肿瘤的面积和周长,用一个空格分开。
# 样例输入 复制
6 99 99 99 99 99 99 99 99 99 50 99 99 99 99 49 49 50 51 99 50 20 25 52 99 40 50 99 99 99 99 99 99 99 99 99 99# 样例输出 复制
9 8
# 思路:
面积的话就是数有多少个小于等于50的,周长的话就是中间那个小于等于50,四周有一个大于50的就算一个。然后从头到尾枚举一遍计数就好。
# 代码C语言:
#include<stdio.h>
int mx[300][300];
int main() {
int n;
scanf("%d",&n);
int ans = 0;
int sum = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
scanf("%d",&mx[i][j]);
if(mx[i][j] <= 50) ans++;
}
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
if(mx[i][j] <= 50 && (mx[i + 1][j] > 50 || mx[i - 1][j] > 50 || mx[i][j + 1] > 50 || mx[i][j - 1] > 50)){
sum++;
}
}
}
printf("%d %d\n",ans,sum);
}
# 3101 平均年龄 (opens new window)
# 题目描述
班上有学生若干名,给出每名学生的年龄(整数),求班上所有学生的平均年龄,按要求输出结果。
# 输入
第一行有一个整数n(1 <= n <= 100),表示学生的人数。其后n行每行有1个整数,取值为15到25。
# 输出
输出一行,为要求的平均年龄,如果为整数,则直接输出该整数,如果为小数,则保留到小数点后1位。
# 样例输入 复制
2 18 17# 样例输出 复制
17.5
# 思路:
没有难点,就是【如果为整数,则直接输出该整数,如果为小数,则保留到小数点后1位】这件事情需要分类一下就好。
# 代码C语言:
#include<stdio.h>
int main(){
int n;
scanf("%d",&n);
int sum = 0;
double aver = 0;
for(int i = 1;i <= n;i++){
int a;
scanf("%d",&a);
sum += a;
}
aver = 1.0 * sum / n;
if(sum % n != 0)
printf("%.1f\n",aver);
else printf("%.0f\n",aver);
}
# 3102 气球来啦 (opens new window)
# 题目描述
本次大赛正式开始了。看着各色各样的气球飘扬在赛场上是多么令人兴奋。作为HDU最好的程序员之一的你,只要你能解决一个非常简单的简单的不能再简单的题目,你就会得到一个漂亮的气球。给你一个运算符(+、-、* 、/,表示加、减、乘、除)和两个正整数,你的任务就是求出它们的运算结果,简单吧,来吧。只要完成任务,漂亮妹妹会马上送给你一个美丽的气球。祝你好运!
# 输入
输入包含多组测试样例,第一行有一个整数T(0 < T < 1000),表示测试样例的组数。然后是T组测试样例,每组包含一个字符C(+、-、* 、/)和两个正整数A和B(0 < A,B < 10000)。当然,A和B是操作数,C是运算符。
# 输出
对于每组测试输出样例其运算结果,当且仅当结果不是整数时,保留2位小数。
# 样例输入 复制
4 + 1 2 - 1 2 * 1 2 / 1 2# 样例输出 复制
3 -1 2 0.50
# 思路:
这道题也很容易,跟着题目写,别忘了分类讨论和换行哦~
# 代码C语言:
#include<stdio.h>
int main(){
int t;
while(~scanf("%d",&t)){
for(int i = 1;i <= t;i++){
char c;
int a,b;
getchar();
scanf("%c %d %d",&c,&a,&b);
switch(c){
case '+':printf("%d\n",a + b);break;
case '-':printf("%d\n",a - b);break;
case '*':printf("%d\n",a * b);break;
case '/':{
if(a % b) printf("%.2f\n",1.0 * a / b);else printf("%d\n",a/b);break;
}
}
}
}
}
# 3103 两倍关系 (opens new window)
# 题目描述
给定2到15个不同的正整数,你的任务是计算这些数里面有多少个数对满足:数对中一个数是另一个数的两倍。 比如给定1 4 3 2 9 7 18 22,得到的答案是3,因为2是1的两倍,4是2个两倍,18是9的两倍。
# 输入
输入包括多组测试数据。每组数据包括一行,给出2到15个两两不同且小于10000的正整数。每一行最后一个数是0,表示这一行的结束后,这个数不属于那2到15个给定的正整数。输入的最后一行只包括一个整数-1,这行表示输入数据的结束,不用进行处理。
# 输出
对每组输入数据,输出一行,给出有多少个数对满足其中一个数是另一个数的两倍。
# 样例输入 复制
1 4 3 2 9 7 18 22 0 2 4 8 10 0 7 5 11 13 1 3 0 -1# 样例输出 复制
3 2 0
# 思路:
简单模拟~下方是笔者大一时写的代码。
# 代码C语言:
#include<stdio.h>
#include<string.h>
int main(){
int num[1000] = {0};
int j,k;
while(1){
int i = 1;
int count = 0;
scanf("%d",&num[0]);
if(num[0]==-1)break;
while(1){
scanf("%d",&num[i++]);
if(num[i-1]==0){
break;
}
}
for(j = 0;j < i-1;j++){
for(k = j+1;k < i-1;k++){
if(num[j]==2*num[k]||num[k]==2*num[j]){
count++;
}
}
}
printf("%d\n",count);
}
return 0;
}
# 3111 最小公倍数 (opens new window)
# 题目描述
给定两个正整数,计算这两个数的最小公倍数。
# 输入
输入包含多组测试数据,每组只有一行,包括两个不大于1000的正整数。
# 输出
对于每个测试数据,给出这两个数的最小公倍数,每个实例输出一行。
# 样例输入 复制
10 14# 样例输出 复制
70
# 思路:
最小公倍数用最大公约数来求就好~
# 代码C语言:
#include<stdio.h>
int gcd(int a,int b){
return b == 0 ? a : gcd(b,a % b);
}
int main(){
int a,b;
while(~scanf("%d %d",&a,&b)){
printf("%d\n",a*b / gcd(a,b));
}
}
# 3112 纸牌 (opens new window)
# 题目描述
一张扑克牌可以放置在桌子的边缘,只要伸出桌子边缘的长度不超过整张牌长度的一半即可。n张牌叠起来放在桌子的边缘,其最长可伸出桌子边缘的长度为1/2+1/4+……+1/(2 * n),输入n,按照题目要求的格式输出n张牌可伸出桌子边缘的最大 。
# 输入
输入文件包括多个测试数据,每个测试数据占一行,为一个非负整数。每个整数都是小于99999的。
# 输出
输出首先包含一个标题,即首先输出下面一行: Cards Overhang (Cards和Overhang间有两个空格) 对输入文件中的每个测试数据,首先输出牌的数目n,然后在输出n张牌最长可伸出桌子边缘的长度,保留小数点后3位有效数字,小数点前至少有一位数。牌的数目右对齐到第5列,长度中的小数点对齐到第12列。
# 样例输入 复制
1 2 3 4 30# 样例输出 复制
Cards Overhang 1 0.500 2 0.750 3 0.917 4 1.042 30 1.997
# 思路:
这道题简单模拟就行,注意输出格式
# 代码C语言:
#include<stdio.h>
double solve(int n){
double sum = 0;
for(int i = 1;i <= n;i++){
sum += 1.0/(2 * i);
}
return sum;
}
int main(){
printf("Cards Overhang\n");
int n;
while(~scanf("%d",&n)){
printf("%5d %9.3f\n",n,solve(n));
}
}
# 3113 肿瘤面积 (opens new window)
# 题目描述
在一个正方形的灰度图片上,肿瘤是一块矩形的区域,肿瘤的边缘所在的像素点在图片中用0表示。其它肿瘤内和肿瘤外的点都用255表示。现在要求你编写一个程序,计算肿瘤内部的像素点的个数(不包括肿瘤边缘上的点)。已知肿瘤的边缘平行于图像的边缘。
# 输入
只有一个测试样例。第一行有一个整数n,表示正方形图像的边长。其后n行每行有n个整数,取值为0或255。整数之间用一个空格隔开。已知n不大于1000。
# 输出
输出一行,该行包含一个整数,为要求的肿瘤内的像素点的个数。
# 样例输入 复制
5 255 255 255 255 255 255 0 0 0 255 255 0 255 0 255 255 0 0 0 255 255 255 255 255 255
# 思路:
毕竟只有一块肿瘤,找到周围一圈0,然后看看里面有多少个255就好。
代码实现方式很多,笔者推荐读者自己写一遍。
笔者采用的方式是,既然是一个矩阵区域,就把右下角0减去左上角0的坐标,然后中间那个矩阵的面积就是肿瘤的面积。
# 代码C语言:
#include<stdio.h>
int mx[1005][1005];
int main(){
int n;
scanf("%d",&n);
int cnt = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
scanf("%d",&mx[i][j]);
if(mx[i][j] == 0) cnt++;
}
}
int b_i = 0,b_j = 0;
int e_i = 0,e_j = 0;
int cnt2 = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
if(mx[i][j] == 0) cnt2++;
if(cnt2 == 1){
b_i = i,b_j = j;
}
if(cnt2 == cnt){
e_i = i,e_j = j;
}
}
}
printf("%d\n",(e_i - b_i - 2) * (e_j - b_j - 2));
}
# 3201 A+B问题 (opens new window)
# 题目描述
读入两个小于10000的正整数A和B,计算A+B。需要注意的是:如果A和B的末尾K(不超过8)位数字相同,请直接输出-1。
# 输入
测试输入包含若干测试数据,每个测试数据占一行,格式为A B K,相邻两数字有一个空格间隔。当A和B同时为0时输入结束,相应的结果不要输出。
# 输出
对每个测试数据输出1行,即A+B的值或者是-1。
# 样例输入 复制
1 2 1 11 21 1 108 8 2 36 64 3 0 0 1# 样例输出 复制
3 -1 -1 100
# 思路:
这道题就是去模拟,如果末尾k位一致就输出-1。怎么判断末尾k位一致,这个就用a % 10、b % 10这种写法,求出a和b的最后一位,然后作比较就行。当然,也可以用字符串来存储a和b去比较会容易一点,但是要写个字符串相加的函数就是了。笔者鼓励读者尽管尝试。
# 代码C语言:
#include<stdio.h>
int solve(int a,int b,int k){
while(a && b){
if(a % 10 != b % 10) break;
k--;
a /= 10,b /= 10;
}
if(a == 0 || b == 0 || k == 0) return 1;
return 0;
}
int main(){
int a,b,k;
while(~scanf("%d %d %d",&a,&b,&k)){
if(!a && !b) break;
if(solve(a,b,k)) printf("-1\n");
else printf("%d\n",a + b);
}
}
# 3202 数字求和 (opens new window)
# 题目描述
给定一个正整数a,以及另外的5个正整数,问题是:这5个整数中,小于a的整数的和是多少?
# 输入
数据有很多行。每一行,只包括6个小于100的正整数,其中第一个正整数就是a。
# 输出
针对每行输入,输出一行,给出一个正整数,是5个数中小于a的数的和。
# 样例输入 复制
10 1 2 3 4 11# 样例输出 复制
10
# 思路:
很简单,注意有多行就好。
# 代码C语言:
#include<stdio.h>
int main(){
int a;
int sum = 0;
while(~scanf("%d",&a)){
sum = 0;
for(int i = 1;i <= 5;i++){
int n;
scanf("%d",&n);
if(n < a) sum += n;
}
printf("%d\n",sum);
sum = 0;
}
}
# 3203 财务管理 (opens new window)
# 题目描述
Larry今年毕业,最终找到了一份工作。他开始挣钱,但是似乎永远不够花的。Larry做出决定,打算投资一些金融证券,以解决他的财务问题。首先需要的就是弄清楚他每个月的开销。Larry有一份银行账目清单,他想看到他有多少钱。请帮助Larry写一个程序,计算他过去的十二个月的账户平均余额。
# 输入
输入一共有12行,每行都是相应月份的银行账户余额。每个数字都是正数,精确到分。这里不包括美元符号。
# 输出
输出一个数字,表示这十二个月的平均值。需要四舍五入到分。数字前面需要包含一个美元符号。没有其他空格或字符。
# 样例输入 复制
100.00 489.12 12454.12 1234.10 823.05 109.20 5.27 1542.25 839.18 83.99 1295.01 1.75# 样例输出 复制
$1581.42
# 思路:
很简单,不评价。
# 代码C语言:
#include<stdio.h>
int main(){
double n;
double sum = 0;
for(int i = 1;i <= 12;i++){
scanf("%lf",&n);
sum += n;
}
double aver = sum / 12;
printf("$%.2lf",aver);
}
# 3204 校门外的树木 (opens new window)
# 题目描述
某校大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴,马路的一端在数轴0的位置,另一端在L的位置;数轴上的每个整数点,即0,1,2,……,L,都种有一棵树。由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。
# 输入
输入的第一行有两个整数L(1 <= L <= 10000)和 M(1 <= M <= 100),L代表马路的长度,M代表区域的数目,L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整数,用一个空格隔开,表示一个区域的起始点和终止点的坐标。注意输入数据可能有很多组。
# 输出
输出包括一行,这一行只包含一个整数,表示马路上剩余的树的数目。
# 样例输入 复制
500 3 150 300 100 200 470 471# 样例输出 复制
298
# 思路:
这道题我们用vis数组存储哪些部分被处理过了,还是很容易的。详情参考代码。
# 代码C语言:
#include<stdio.h>
int vis[10005];
int main(){
int l,m;
scanf("%d %d",&l,&m);
for(int i = 1;i <= m;i++){
int begin,end;
scanf("%d %d",&begin,&end);
for(int j = begin;j <= end;j++){
vis[j]++;
}
}
int cnt = 0;
for(int i = 1;i <= l;i++){
if(vis[i]) cnt++;
}
printf("%d\n",l - cnt + 1);
}
# 3205 直角三角形 (opens new window)
# 题目描述
当你拥有计算机后,数学运算就变得非常简单了。举个例子来说,你可能知道直角三角形的定义:如果3边a,b,c(假定c为最长的边,也就是斜边)满足如下关系:a * a + b * b = c * c,那么这个就是直角三角形。这就是所谓的毕达哥拉斯(Pythagora)定律。 这里如果给定其中的两个边,如何计算第三边的长度。
# 输入
输入包含一些三角形的描述,每个描述占一行,包括了三个整数a,b和c,表示对应的直角三角形的三个边。三个数字当中有一个等于-1(表示未知的边),其余两个都是正数(表示已知的边)。如果a=b=c=0表示输入结束。
# 输出
对于每个输入的三角形,首先要输出三角形的序号,如输出样例所示。如果不能构成直角三角形,输出“Impossible.”。否则,输出为“s = L”,其中s是未知边的名称(a,b或c),L为其长度,精确到小数点后三位。 每个测试数据后输出一个空行。
# 样例输入 复制
3 4 -1 -1 2 7 5 -1 3 0 0 0# 样例输出 复制
Triangle #1 c = 5.000 Triangle #2 a = 6.708 Triangle #3 Impossible.
# 思路:
这道题也很简单,直接算就好,注意保留小数位和格式。
# 代码C语言:
#include<stdio.h>
#include<math.h>
int main(){
double a,b,c;
int t = 0;
while(~scanf("%lf %lf %lf",&a,&b,&c)){
t++;
if(!a && !b && !c) break;
printf("Triangle #%d\n",t);
if(a == -1){
a = sqrt(c * c - b * b);
if(a < c && b < c){
printf("a = %.3f\n",a);
}else{
printf("Impossible.\n");
}
}
if(b == -1){
b = sqrt(c * c - a * a);
if(a < c && b < c){
printf("b = %.3f\n",b);
}else{
printf("Impossible.\n");
}
}
if(c == -1){
c = sqrt(a * a + b * b);
if(a < c && b < c){
printf("c = %.3f\n",c);
}else{
printf("Impossible.\n");
}
}
printf("\n")
}
}
# 3206 化验诊断 (opens new window)
# 题目描述
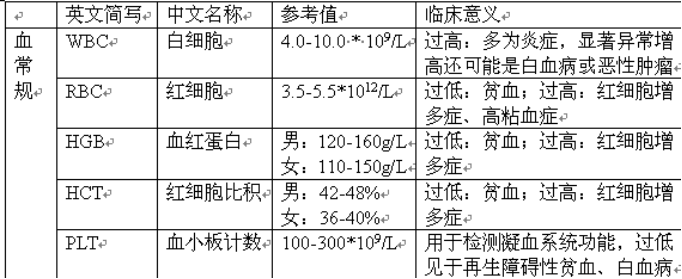
下表是进行血常规检验的正常值参考范围,及化验值异常的临床意义:
血常规检验正常值参考范围列表
给定一张化验单,判断其所有指标是否正常,如果不正常,统计有几项不正常。化验单上的值必须严格落在正常参考值范围内,才算是正常。正常参考值范围包括边界,即落在边界上也算正常。
# 输入
输入的第一行包含一个正整数k(0 < k < 100),表示有k组测试数据;接下来k行,每行包含一组测试数据。每组测试数据第一项是一个英文单词(male,男或者female,女),表示受测者的性别;第二项是白细胞的值(以109/L为单位);第三项是红细胞的值(以1012/L为单位);第四项是血红蛋白的值(以g/L为单位);第五项是红细胞比积的值(以%为单位);第六项是血小板计数的值(以109/L为单位)。每两项用一个空格分开。
# 输出
对于每组测试数据,输出一行。如果所有检验项目正常,则输出:normal;否则输出不正常的项的数目。
# 样例输入 复制
2 female 4.5 4.0 115 37 200 male 3.9 3.5 155 36 301# 样例输出 复制
normal 3
# 思路:
这道题就是实现比较麻烦,是个比较多的模拟,下面献上笔者大一的代码~读者自行模拟即可。
# 代码C语言:
#include<stdio.h>
#include<math.h>
int main(){
int k;
char str[1000];
double wbc,rbc;
int hgb,hct,plt;
scanf("%d",&k);
getchar();
while(k--){
int flag[5] = {0};
int count = 0;
int sign = 0;
int i;
//gets(str);
scanf("%s %lf %lf %d %d %d",str,&wbc,&rbc,&hgb,&hct,&plt);
if(str[0]=='f'){
if(fabs(wbc-4.0)<1e-6||(wbc>=4.0&&wbc<=10.0)||fabs(wbc-10.0)<1e-6){
flag[0] = 0;
}else{
flag[0] = 1;
count++;
}
if(fabs(rbc-3.5)<1e-6||(rbc>=3.5&&rbc<=5.5)||fabs(rbc-5.5)<1e-6){
flag[1] = 0;
}else{
flag[1] = 1;
count++;
}
if(hgb>=110&&hgb<=150){
flag[2] = 0;
}else{
flag[2] = 1;
count++;
}
if(hct>=36&&hct<=40){
flag[3] = 0;
}else{
flag[3] = 1;
count++;
}
if(plt>=100&&plt<=300){
flag[4] = 0;
}else{
flag[4] = 1;
count++;
}
}
else if(str[0]=='m'){
if(fabs(wbc-4.0)<1e-6||(wbc>=4.0&&wbc<=10.0)||fabs(wbc-10.0)<1e-6){
flag[0] = 0;
}else{
flag[0] = 1;
count++;
}
if(fabs(rbc-3.5)<1e-6||(rbc>=3.5&&rbc<=5.5)||fabs(rbc-5.5)<1e-6){
flag[1] = 0;
}else{
flag[1] = 1;
count++;
}
if(hgb>=120&&hgb<=160){
flag[2] = 0;
}else{
flag[2] = 1;
count++;
}
if(hct>=42&&hct<=48){
flag[3] = 0;
}else{
flag[3] = 1;
count++;
}
if(plt>=100&&plt<=300){
flag[4] = 0;
}else{
flag[4] = 1;
count++;
}
}
for(i = 0;i < 5;i++){
if(flag[i] == 1)
sign = 1;
}
if(sign == 0){
printf("normal\n");
}else{
printf("%d\n",count);
}
}
return 0;
}
# 3207 数字阶梯 (opens new window)
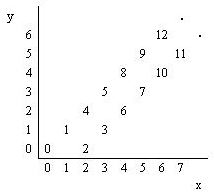
# 题目描述
从坐标(0,0)出发,在平面上写下所有非负整数0,1,2,…,如下图所示,例如1、2和3分别是在(1,1)、(2,0)和(3,1)坐标处写下的。
数字阶梯
编写一个程序,给定坐标(x,y),输出对应的整数(如果存在的话),输入文件中的x,y坐标范围都是0~5000。
# 输入
输入文件的第一行为正整数N,表示输入文件中测试数据的数目。接下来是N个测试数据,每个测试数据占一行,包含两个整数:x和y,代表平面上的坐标(x,y)。
# 输出
对输入文件中每一行所表示的坐标点,输出在该点的非负整数,如果没有对应整数,输出“No Number”。
# 样例输入 复制
3 4 2 6 6 3 4# 样例输出 复制
6 12 No Number
# 思路:
这道题观察数轴上的一次函数,得出规律就行。
# 代码C语言:
#include<stdio.h>
int main(){
int n;
scanf("%d",&n);
while(n--){
int x,y;
scanf("%d %d",&x,&y);
if(x==y||(x-y)==2){
if(x==y){
if(x%2==0){
printf("%d\n",2*x);
}else{
printf("%d\n",2*(x-1)+1);
}
}
else{
if(x%2==0){
printf("%d\n",x+y);
}else{
printf("%d\n",x+y-1);
}
}
}else{
printf("No Number\n");
}
}
return 0;
}
# 3208 一个简单的化学问题 (opens new window)
# 题目描述
你们化学实验室的助教是一名非常热心的研究生,他要求你在混合实验时监测整个实验室每分钟的温度,以便能够绘制出整个实验室的温度变化率。 作为一名有前途的计算机科学家,你知道可以自动处理这个过程。因此,你写了一段程序,在实验的时候运行在实验室的笔记本电脑上。你将写一个程序,输入每个观测到的温度,程序将自动计算当前温度与前一个温度间的差值,然后输出它。
# 输入
输入一系列的温度,每个温度占一行,温度的范围从-10 到200,温度精确到小数点后两位。数字999表示输入数据结束。数据集中至少有两个温度。
# 输出
你的程序将输出一系列温度的差值。差值需要保留小数点两位,并且没有前导0(除非小于1,例如0.01)或空格。 所有输出结束后,输出一行End of Output。
# 样例输入 复制
10.0 12.05 30.25 20 999# 样例输出 复制
2.05 18.20 -10.25 End of Output
# 思路:
简单模拟,不再多说。
# 代码C语言:
#include<stdio.h>
double a,b;
int main(){
scanf("%lf",&a);
while(~scanf("%lf",&b)){
if(a == 999 || b == 999) break;
printf("%.2lf\n",b - a);
a = b;
}
printf("End of Output\n");
}
# 总结
- 题目难度简单,推荐读者尽量不看题解自行思考。
- 考察的都是模拟方面的知识,除了 3007 装箱问题 考察了贪心的想法,那道题目较为难写,水平不足可以暂时跳过。
- 可以参考学习一下笔者的部分代码风格。